题目内容
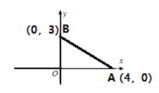
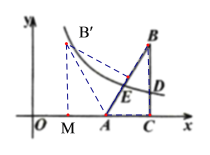
【题目】如图,在平面直角坐标系中,![]() 的直角边
的直角边![]() 在
在![]() 轴上,
轴上,![]() ,反比例函数
,反比例函数![]()
![]() 的图象与
的图象与![]() 边相交于点
边相交于点 ,与
,与![]() 边相交于点
边相交于点![]() .
.
(1)求这个反比例函数的解析式;
(2)若点![]() 是
是![]() 的中点,
的中点,![]() .
.
①求![]() 的度数;
的度数;
②将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,点
,点![]() 的对应点为
的对应点为![]() ,直接写出
,直接写出![]() 的坐标,并判断点
的坐标,并判断点![]() 是否在此反比例函数的图象上.
是否在此反比例函数的图象上.

【答案】(1)![]() ;(2)①
;(2)①![]() ,②
,②![]() ,在图像上
,在图像上
【解析】
(1)根据待定系数法,即可得到答案;
(2)①先求出C,A的坐标以及点B的横坐标,从而求出点E的横坐标,进而求出点E的纵坐标,然后求出BC的长,根据三角函数的定义,即可求解;②过点B′作B′M⊥x轴于点M,根据旋转的性质,得∠B′AM=60°,B′A 的长,通过解直角三角形,得B′M,AM的值,进而即可得到答案.
(1)把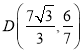 代入
代入![]() ,得:k=
,得:k=![]() ×
×![]() =
=![]() ,
,
∴这个反比例函数的解析式为:![]() ;
;
(2)①∵![]() 的直角边
的直角边![]() 在
在![]() 轴上,
轴上,![]() ,
,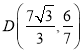 ,
,![]() ,
,
∴C(![]() ,0),A(
,0),A(![]() ,0),点B的横坐标为
,0),点B的横坐标为![]() ,
,
∵点![]() 是
是![]() 的中点,
的中点,
∴点E的横坐标为:(![]() +
+![]() )÷2=
)÷2=![]() ,
,
∴点E的纵坐标为:![]() ,
,
∴点B的纵坐标为:2,即BC=2,
∴在![]() 中,tan∠BAC=
中,tan∠BAC=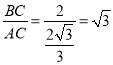 ,
,
∴∠BAC=60°;
②过点B′作B′M⊥x轴于点M,
∵![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,点
,点![]() 的对应点为
的对应点为![]()
∵∠BAC=∠BAB′=60°,B′A=BA=2AC=![]() ,
,
∴∠B′AM=60°,B′M= B′Asin60°=![]() ×
×![]() =2,AM= B′Acos60°=
=2,AM= B′Acos60°=![]() ×
×![]() =
=![]() ,
,
∵A(![]() ,0),
,0),
∴B′(![]() ,2),
,2),
∵![]() ,
,
∴![]() 在此反比例函数的图象上.
在此反比例函数的图象上.

【题目】某区八年级有3000名学生参加“爱我中华”知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了部分学生的得分进行统计.
成绩x(分) | 频数 | 频率 |
50≤x<60 | 10 | a |
60≤x<70 | 16 | 0.08 |
70≤x<80 | b | 0.20 |
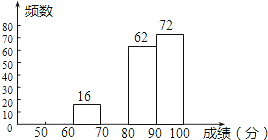
请你根据以上的信息,回答下列问题:
(1) a= ,b= ;
(2) 在扇形统计图中,“成绩x满足50≤x<60”对应扇形的圆心角大小是 ;
(3) 若将得分转化为等级,规定:50≤x<60评为D,60≤x<70评为C,70≤x<90评为B,90≤x<100评为A.这次全区八年级参加竞赛的学生约有 学生参赛成绩被评为“B”?