题目内容
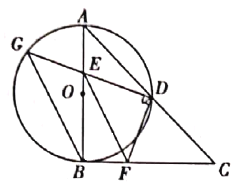
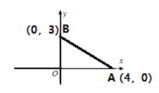
【题目】如图,已知点A的坐标为(4,0),点B的坐标为(0,3),在第一象限内找一点P(a,b) ,使△PAB为等边三角形,则2(a-b)=___________.
【答案】![]()
【解析】
根据A、B坐标求出直线AB的解析式后,求得AB中点M的坐标,连接PM,在等边△PAB中,M为AB中点,所以PM⊥AB,![]() ,再求出直线PM的解析式,求出点P坐标;在Rt△PAM中,AP=AB=5,
,再求出直线PM的解析式,求出点P坐标;在Rt△PAM中,AP=AB=5,![]() ,即
,即![]() 且a>0,解得a>0,即
且a>0,解得a>0,即![]() ,将a代入直线PM的解析式中求出b的值,最后计算2(a-b)的值即可;
,将a代入直线PM的解析式中求出b的值,最后计算2(a-b)的值即可;
解:∵A(4,0),B(0,3),
∴AB=5,
设![]() ,
,
∴![]() ,
,
∴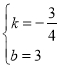 ,
,
∴![]() ,
,
∵A(4,0) B(0,3) ,
∴AB中点![]() ,连接PM,
,连接PM,
在等边△PAB中,M为AB中点,
∴PM⊥AB,![]() ,
,
∴![]() ,
,
∴设直线PM的解析式为![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
在Rt△PAM中,AP=AB=5,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵a>0,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
【题目】某中学抽取了40名学生参加“平均每周课外阅读时间”的调查,由调查结果绘制了如下不完整的频数分布表和扇形统计图.
组别 | 时间/小时 | 频数/人数 |
A组 |
| 2 |
B组 |
| m |
C组 |
| 10 |
D组 |
| 12 |
E组 |
| 7 |
F组 |
| 4 |
频数分布表
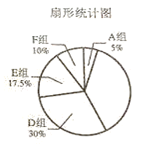
请根据图表中的信息解答下列问题:
(1)求频数分布表中m的值;
(2)求B组,C组在扇形统计图中分别对应扇形的圆心角度数,并补全扇形统计图;
(3)已知F组的学生中,只有1名男生,其余都是女生,用列举法求以下事件的概率:从F组中随机选取2名学生,恰好都是女生。