题目内容
已知△ABC中,∠ACB=90°,AB=2,CB=1,将△ABC沿水平线(AB所在的直线)作翻转运动.下图是△ABC二次翻转形成的图形.(1)第一次翻转后的图形△BC′A′是由△ABC按顺时针方向旋转所得的,那么哪一点是旋转中心?旋转了多少度?
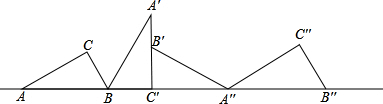
(2)在下图中,画出△ABC第三次翻转后的图形,请你仔细观察图中的△ABC与由它第三次翻转后的图形,想一想他们之间还可以是怎样的变换,请将它完整地表达出来.
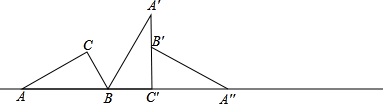
分析:(1)根据旋转的定义即可解答;
(2)首先作出图形,由△ABC到△A″B″C″可以进行平移变换,平移的距离是BB″,求得AC的长度即可求得.
(2)首先作出图形,由△ABC到△A″B″C″可以进行平移变换,平移的距离是BB″,求得AC的长度即可求得.
解答:解:(1)旋转中心是点B,旋转了120°;
(2)图形:
AC=
=
=
.
∴BB″=1+
+2=3+
.
∴△A″B″C″是由△ABC沿着AB所指的方向(即沿着水平线)向右平移了(3+
)得到.
(2)图形:

AC=
| AB2-CB2 |
| 22-12 |
| 3 |
∴BB″=1+
| 3 |
| 3 |
∴△A″B″C″是由△ABC沿着AB所指的方向(即沿着水平线)向右平移了(3+
| 3 |
点评:本题主要考查了旋转的作图,旋转的性质,正确作图是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 情况;若不可能,请说明理由.
情况;若不可能,请说明理由. 已知△ABC中,DE∥BC,EF∥AB,AB=3,BC=6,AD:DB=2:1,则四边形DBFE的周长为
已知△ABC中,DE∥BC,EF∥AB,AB=3,BC=6,AD:DB=2:1,则四边形DBFE的周长为 如图所示,已知△ABC中,AB=AC,以AB为直径作⊙O交BC于D,交AC于E,过D作DF⊥AC于F
如图所示,已知△ABC中,AB=AC,以AB为直径作⊙O交BC于D,交AC于E,过D作DF⊥AC于F 如图,已知△ABC中,AB=AC,AB垂直平分线交AC于D,连接BE,若∠A=40°,则∠EBC=( )
如图,已知△ABC中,AB=AC,AB垂直平分线交AC于D,连接BE,若∠A=40°,则∠EBC=( )