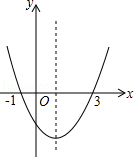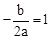��Ŀ����
��ͼ����ֱ����ϵ�У�ֱ��AB��x���ڵ�A��5��0������y���ڵ�B��AO�ǡ�M��ֱ�������Բ��AB�ڵ�C����AC=3��ȡBO���е�D������CD��MD��OC��
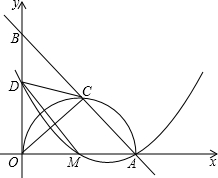
��1����֤��CD�ǡ�M�����ߣ�
��2�����κ�����ͼ����D��M��A����Գ�������һ����P������PD��PM�����PDM���ܳ���Сʱ��P�����ꣻ
��3���ڣ�2���������£�����PDM���ܳ���Сʱ�����������Ƿ���ڵ�Q��ʹ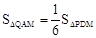 �������ڣ������Q�����ꣻ�������ڣ���˵�����ɡ�
�������ڣ������Q�����ꣻ�������ڣ���˵�����ɡ�

��1����֤��CD�ǡ�M�����ߣ�
��2�����κ�����ͼ����D��M��A����Գ�������һ����P������PD��PM�����PDM���ܳ���Сʱ��P�����ꣻ
��3���ڣ�2���������£�����PDM���ܳ���Сʱ�����������Ƿ���ڵ�Q��ʹ
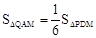 �������ڣ������Q�����ꣻ�������ڣ���˵�����ɡ�
�������ڣ������Q�����ꣻ�������ڣ���˵�����ɡ��⣺��1��֤��������CM��
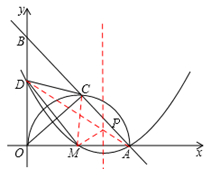
��OA Ϊ��Mֱ�������OCA=90�㡣���OCB=90�㡣
��DΪOB�е㣬��DC=DO�����DCO=��DOC��
��MO=MC�����MCO=��MOC��
��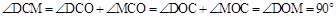 ��
��
�֡ߵ�C�ڡ�M�ϣ���DC�ǡ�M�����ߡ�
��2����A�����꣨5��0����AC=3
����Rt��ACO��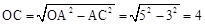 ��
��
��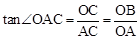 ����
����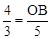 �����
����� 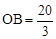 ��
��
�֡�DΪOB�е㣬��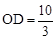 ����D������Ϊ��0��
����D��������0��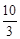 )��
)��
����AD����ֱ��AD�Ľ���ʽΪy=kx+b������
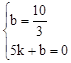 ���
���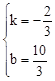 ��
��
��ֱ��ADΪ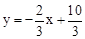 ��
��
�߶��κ�����ͼ���M��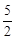 ��0)��A(5��0)��
��0)��A(5��0)��
�������߶Գ���x=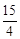 ��
��
�ߵ�M��A����ֱ��x=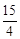 �Գƣ���ֱ��AD��ֱ��x=
�Գƣ���ֱ��AD��ֱ��x=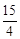 ���ڵ�P��
���ڵ�P��
��PD+PMΪ��С��
�֡�DMΪ�����������������ĵ�PΪֱ��AD��ֱ��x=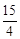 �Ľ��㡣
�Ľ��㡣
��x=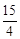 ʱ��
ʱ��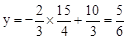 ��
��
��P���������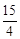 ��
��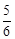 ����
����
��3�����ڡ�
��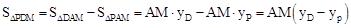 ��
��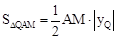
���ɣ�2��֪D��0��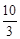 )��P��
)��P��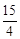 ��
��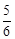 ����
����
����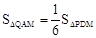 ����
����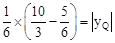 �����yQ=��
�����yQ=��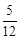 ��
��
�߶��κ�����ͼ���M(0��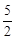 )��A(5��0����
)��A(5��0����
������κ�������ʽΪ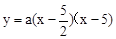 ��
��
�֡߸�ͼ�����D��0��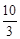 )����
)����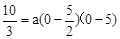 �����a=
�����a=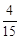 ��
��
����κ�������ʽΪ ��
��
�֡�Q�����������ϣ���yQ=��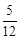 ��
��
�൱yQ=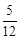 ʱ��
ʱ��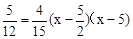 �����x=
�����x=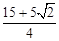 ��x=
��x=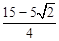 ��
��
��yQ=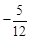 ʱ��
ʱ��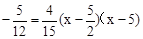 �����x=
�����x=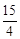 ��
��
���Q��������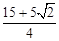 ��
��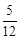 )����
)����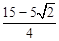 ��
��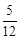 )����
)����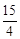 ��
��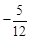 ����
����

��OA Ϊ��Mֱ�������OCA=90�㡣���OCB=90�㡣
��DΪOB�е㣬��DC=DO�����DCO=��DOC��
��MO=MC�����MCO=��MOC��
��
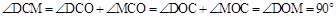 ��
���֡ߵ�C�ڡ�M�ϣ���DC�ǡ�M�����ߡ�
��2����A�����꣨5��0����AC=3
����Rt��ACO��
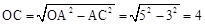 ��
����
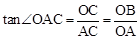 ����
����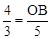 �����
����� 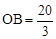 ��
���֡�DΪOB�е㣬��
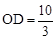 ����D��������0��
����D��������0��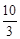 )��
)������AD����ֱ��AD�Ľ���ʽΪy=kx+b������
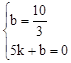 ���
���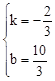 ��
����ֱ��ADΪ
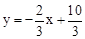 ��
���߶��κ�����ͼ���M��
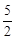 ��0)��A(5��0)��
��0)��A(5��0)���������߶Գ���x=
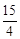 ��
���ߵ�M��A����ֱ��x=
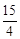 �Գƣ���ֱ��AD��ֱ��x=
�Գƣ���ֱ��AD��ֱ��x=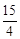 ���ڵ�P��
���ڵ�P����PD+PMΪ��С��
�֡�DMΪ�����������������ĵ�PΪֱ��AD��ֱ��x=
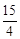 �Ľ��㡣
�Ľ��㡣��x=
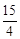 ʱ��
ʱ��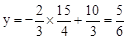 ��
����P���������
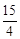 ��
��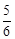 ����
������3�����ڡ�
��
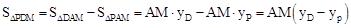 ��
��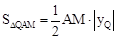
���ɣ�2��֪D��0��
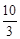 )��P��
)��P��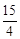 ��
��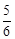 ����
��������
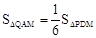 ����
����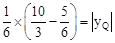 �����yQ=��
�����yQ=��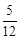 ��
���߶��κ�����ͼ���M(0��
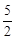 )��A(5��0����
)��A(5��0����������κ�������ʽΪ
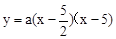 ��
���֡߸�ͼ�����D��0��
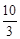 )����
)����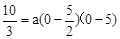 �����a=
�����a=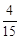 ��
������κ�������ʽΪ
 ��
���֡�Q�����������ϣ���yQ=��
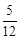 ��
���൱yQ=
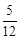 ʱ��
ʱ��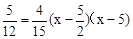 �����x=
�����x=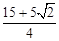 ��x=
��x=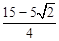 ��
����yQ=
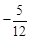 ʱ��
ʱ��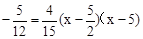 �����x=
�����x=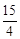 ��
�����Q��������
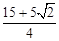 ��
��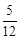 )����
)����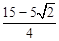 ��
��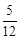 )����
)����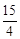 ��
��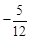 ����
���������������1������CM�����Եó�CM=OM�����С�MOC=��MCO����OAΪֱ�������С�ACO=90�㣬DΪOB���е㣬����CD=OD����DOC=��DCO���ɡ�DOC+��MOC=90��Ϳ��Եó���DCO+��MCO=90����ó����ۡ�
��2�������������Եó�
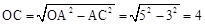 ��
��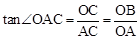 ���Ӷ����OB��ֵ������D��OB���е�Ϳ������D�����꣬�ɴ���ϵ�����Ϳ�����������ߵĽ���ʽ������Գ��ᣬ������ԳƵ���������AD���Գ�����P�������AD�Ľ���ʽ�Ϳ������P�����ꡣ
���Ӷ����OB��ֵ������D��OB���е�Ϳ������D�����꣬�ɴ���ϵ�����Ϳ�����������ߵĽ���ʽ������Գ��ᣬ������ԳƵ���������AD���Գ�����P�������AD�Ľ���ʽ�Ϳ������P�����ꡣ��3������
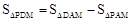 ��
��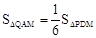 ���Q�������꣬������κ�������ʽ������ú����ꡣ
���Q�������꣬������κ�������ʽ������ú����ꡣ
��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
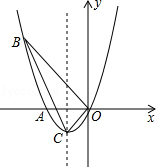
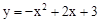 ��ͼ������ƽ��1����λ��������ƽ��2����λ����ƽ�ƺ�������ߵĽ���ʽ��ƽ�ƺ������ߵ���״���䣩��
��ͼ������ƽ��1����λ��������ƽ��2����λ����ƽ�ƺ�������ߵĽ���ʽ��ƽ�ƺ������ߵ���״���䣩��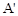 ��
��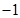 ��3����������ƽ��2����λ�õ�
��3����������ƽ��2����λ�õ�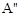 ��
��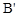 ��0��4����������ƽ��2����λ�õ�
��0��4����������ƽ��2����λ�õ� ��0��2����
��0��2����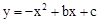 ��
��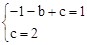 ����ã�
����ã�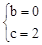 ��
�� ��
��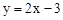 ����ƽ��3����λ��������ƽ��1����λ����ƽ�ƺ��ֱ�ߵĽ���ʽ��
����ƽ��3����λ��������ƽ��1����λ����ƽ�ƺ��ֱ�ߵĽ���ʽ��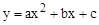 ����A��B��C���㣬����ΪF��
����A��B��C���㣬����ΪF��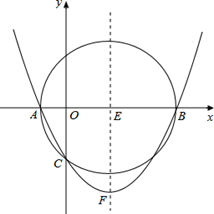
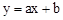 ��������
��������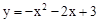 �Ķ���P����ͼ��ʾ��
�Ķ���P����ͼ��ʾ��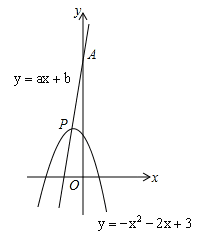
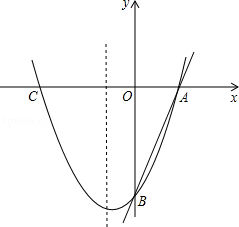
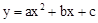 ��ͼ����ͼ��ʾ����һ�κ���
��ͼ����ͼ��ʾ����һ�κ���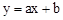 �뷴��������
�뷴��������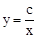 ��ͬһƽ��ֱ������ϵ�еĴ���ͼ��Ϊ�� ��
��ͬһƽ��ֱ������ϵ�еĴ���ͼ��Ϊ�� ��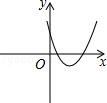
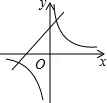
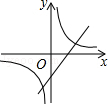
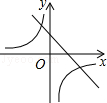
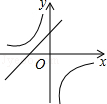
 ��
�� �dz�����
�dz����� ��ֻ��һ�����㣬��
��ֻ��һ�����㣬�� ��ij������������ͼ���ϣ�Ҫʹ�÷����������Ͷ��κ���
��ij������������ͼ���ϣ�Ҫʹ�÷����������Ͷ��κ��� ��
�� ���㣬��
���㣬�� ��
�� ����
����