题目内容
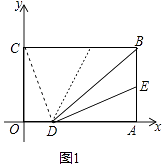
【题目】如图，EF过矩形ABCD对角线的交点O ， 且分别交AB、CD于E、F ， 那么阴影部分的面积与矩形ABCD面积的大小关系是什么？
【答案】解答：解：阴影部分的面积与矩形ABCD面积的 
∵四边形为矩形，∴OB＝OD＝OA＝OC ， 在△EBO与△FDO中，∠EOB＝∠DOF ， OB＝OD ， ∠EBO＝∠FDO ， △EBO≌△FDO ， ∴S阴影部分的面积＝ 
，∵△AOB与△ABC同底且△AOB的高是△ABC高的 
，∴ 
S矩形ABCD ．
【解析】本题主要根据矩形的性质，得△EBO≌△FDO ， 再由△AOB与△OBC同底等高，得出结论．
【考点精析】通过灵活运用矩形的性质，掌握矩形的四个角都是直角，矩形的对角线相等即可以解答此题．
练习册系列答案
相关题目
