题目内容
【题目】在平面直角坐标系中B(3,2),BC⊥y轴于C,BA⊥x轴于A,点E在线段AB上从B向A以每秒1个单位的速度运动,运动时间为t秒(0<t<2).将BE沿BD折叠,使E点恰好落在BC上的F处.
(1)如图1,若E为AB的中点,请直接写出F、D两点的坐标:F( , ) D( , )
(2)如图1,连接CD,在(1)的条件下,求证:CD=FD.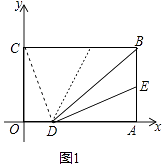
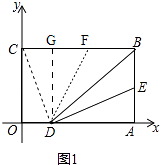
(3)如图2,在E点运动的同时,M点在OC上从C向O运动,N点在OA上从A向O运动,M的运动速度为每秒3个单位,N的运动速度为每秒a个单位.在运动过程中,△CMF能与△ANE全等吗?若能,求出此时a与t的值,若不能,请说明理由.
【答案】
(1)2;2;1;0
(2)
解:如图1,过点D作DG⊥BC于G,
由折叠得,DE=DF,∠BED=∠BFD,
∴∠AED=DFC,
在△AED和△GFD中 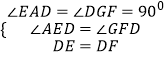 ,
,
∴△AED≌△GFD,
∴GF=AE=1,
∵CF=2,
∴CG=1,
∴CG=FG,
∵DG⊥CG,
∴CD=FD
(3)
解:能全等,即:△CMF≌△AEN,
理由:
∵M点在OC上从C向O运动,N点在OA上从A向O运动,M的运动速度为每秒3个单位,N的运动速度为每秒a个单位,点E在线段AB上从B向A以每秒1个单位的速度运动,
∴CM=3t,AN=at,BE=t,
∴AE=2﹣t,
∵将BE沿BD折叠,使E点恰好落在BC上的F处,
∴BF=BE=t,
∴CF=BC﹣BF=3﹣t,
∵BF=BE,BC≠AB,
∴AE=CF,
∵△CMF与△ANE全等
∴△CMF≌△AEN,
∴CM=AE,CF=AN,
∴3t=2﹣t,3﹣t=at,
∴t= ![]() ,a=5.
,a=5.
【解析】解:(1)∵四边形ABCD是矩形,且B(3,2),
∴OA=BC=3,OC=AB=2,
∵E为AB的中点,
∴AE=BE=1,
由折叠得,BF=BE=1,
∴CF=2,
∴F(2,2),
如图1,
过点D作DG⊥BC于G,
由折叠得,DE=DF,∠BED=∠BFD,
∴∠AED=DFC,
在△AED和△GFD中 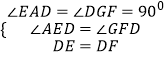 ,
,
∴△AED≌△GFD,
∴AD=DG=OC=2,
∴OD=1,
∴D(1,0),
所以答案是:2,2,1,0;





