题目内容
【题目】杂技团进行杂技表演，演员从跷跷板右端A处（OA=1米）弹跳到人梯顶端椅子B处，借助其弹性可以将演员弹跳到离地面最高处点P（ 
， 
）
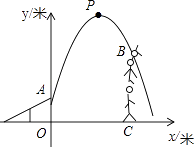
（1）若将其身体（看成一个点）的路线为抛物线的一部分，求抛物线的解析式．
（2）在一次表演中，已知人梯高BC=3.4米，演员弹跳到最高处点P后落到人梯顶端椅子B处算表演成功，为了这次表演成功，人梯离起跳点A的水平距离OC是多少米？请说明理由．
【答案】
（1）
解：设抛物线解析式为y=a（x﹣h）2+k，
∵最高处点P（ 
， 
），
∴h= ，k= ，
∴y=a（x﹣ ）2+ ，
∵OA=1米，
∴点A的坐标为（0，1），
∴1=a× 
+ ，
解得：a=﹣ 
，
∴y=﹣ （x﹣ ）2+ =﹣ x2+3x+1；
（2）
解：∵BC=3.4米，
∴B的纵坐标为3.4，
∴3.4=﹣ x2+3x+1，
解得：x=4或1，
∴人梯离起跳点A的水平距离OC是4米．
【解析】（1）设抛物线解析式为y=a（x﹣h）2+k，由已知条件可知h和k的值，再把点A的坐标代入求出a的值即可；（2）由BC=3.4米，可知点B的纵坐标为3.4，把其纵坐标代入抛物线的解析式求出其横坐标，即可得到人梯离起跳点A的水平距离OC．
【考点精析】本题主要考查了二次函数的图象和二次函数的性质的相关知识点，需要掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小才能正确解答此题．
【题目】骑共享单车已成为人们喜爱的一种绿色出行方式．已知A、B、C三家公司的共享单车都是按骑车时间收费，标准如下：
公司 | 单价（元/半小时） | 充值优惠 |
A | m | 充20元送5元，即：充20元实得25元 |
B | m－0.2 | 无 |
C | 1 | 充20元送20元，即：充20元实得40元 |
（注：使用这三家公司的共享单车，不足半小时均按半小时计费．用户的账户余额长期有效，但不可提现．）
4月初，李明注册成了A公司的用户，张红注册成了B公司的用户，并且两人在各自账户上分别充值20元．一个月下来，李明、张红两人使用单车的次数恰好相同，且每次都在半小时以内，结果到月底李明、张红的账户余额分别显示为5元、8元．
（1）求m的值；
（2）5月份，C公司在原标准的基础上又推出新优惠：每月的月初给用户送出5张免费使用券（1
次用车只能使用1张券）．如果王磊每月使用单车的次数相同，且在30次以内，每次用车都不超过
半小时. 若要在这三家公司中选择一家并充值20元，仅从资费角度考虑，请你帮他作出选择，并说
明理由．
