Question

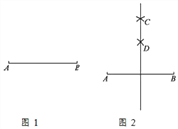
【题目】探究：小明在求同一坐标轴上两点间的距离时发现，对于平面直角坐标系内任意两点P1x1,y1，P2x2,y2，可通过构造直角三角形利用图1得到结论：，他还利用图2证明了线段P1P2的中点Px,y的坐标公式：

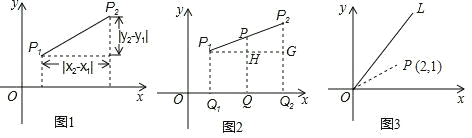
（1）已知点M2,1,N2,5，则线段MN长度为 ；

（2）请求出以点A2,2,B2,0,C3,1，D为顶点的平行四边形顶点D的坐标；

（3）如图3，OL满足y2xx0，点P2,1是OL与x轴正半轴所夹的内部一点，请在OL、x轴上分别找出点E、F，使PEF的周长最小，求出周长的最小值.

Answer 1

【答案】（1）；（2）（－3，3）或（7，1）或（－1，－3）；（3）△PEF周长的最小值是4.

【解析】

（1）直接利用两点间距离公式可求得MN的长；

（2）分AB、AC、BC为对角线，可求得其中心的坐标，再利用中点坐标公式可求得D点坐标；

（3）设P点关于x轴的对称点为P1，P点关于直线y=2x的对称点为P2，连接PP1交x轴于点H，连接PP2交直线y=2x于点G，连接P1P2，分别交x轴、直线y=2x于点F、E，由对称性知此时△PEF的周长最小，等于P1P2的长；由于PP2⊥OG，于是根据两直线垂直有，可设直线PP2的解析式为，把P点坐标代入可求得b，于是直线PP2的解析式可得，联立直线PP2和OG的解析式可求得G点坐标，因为G为PP2的中点，由中点坐标公式可求得P2点的坐标，而P1的坐标为（2，－1），最后再用两点间距离公式求出即可.

解：（1）∵M（2，﹣1），N（﹣2，5），

∴MN==，

故答案为：；

（2）∵A（2，2），B（﹣2，0），C（3，﹣1），

∴当AB为平行四边形的对角线时，其对称中心坐标为（0，1），

设D（x，y），则x+3=0，y+（﹣1）=2，解得x=﹣3，y=3，

∴此时D点坐标为（﹣3，3）；

当AC为对角线时，同理可求得D点坐标为（7，1）；

当BC为对角线时，同理可求得D点坐标为（﹣1，﹣3），

综上可知D点坐标为（﹣3，3）或（7，1）或（﹣1，﹣3）；

（3）如图，设P点关于x轴的对称点为P1，P点关于直线y=2x的对称点为P2，连接PP1交x轴于点H，连接PP2交直线y=2x于点G，连接P1P2，分别交x轴、直线y=2x于点F、E，由对称性知，PE=P2E，PF=P1F，PE+EF+PF=P2E+EF+P1F=P1P2，

此时△PEF的周长最小，等于P1P2的长.

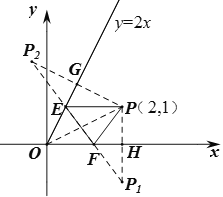
∵PP2⊥OG，OG的解析式为y=2x，

∴可设直线PP2的解析式为，

把P点坐标（2,1）代入上述解析式，得b=2，

∴直线PP2的解析式为，

联立方程组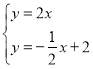，解得.

∴G点的坐标为（）.

设P2点的坐标为（a，b），因为G是PP2的中点，所以，

解得：，所以P2点的坐标为（），

又因为P1的坐标是（2,－1），

所以由两点距离公式，得.

故△PEF周长的最小值是4.