Question

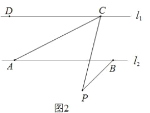
【题目】如图，已知正三角形ABC与正三角形CDE，若∠DBE=66°，则∠ADB度数为__________.

Answer 1

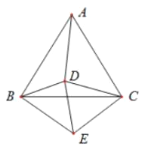
【答案】126°

【解析】

现根据正三角形ABC与正三角形CDE证出△BCE△ADC，从而得出∠ADC=∠BEC∠BED+60°;再根据三角形的内角和得出∠BDE=114°-∠BED，再根据∠ADB=360°-∠ADC-∠BDE-∠EDC即可得出∠ADB的度数。

∵正三角形ABC与正三角形CDE

∴CD=CE,BC=AC, ∠DEC=∠EDC=∠DCE=60°

∴∠EDC-∠BCD=∠DCE-∠BCD

∴∠BCE=∠DCA

在△BCE和△ADC中;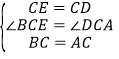

∴△BCE△ADC ∴∠ADC=∠BEC;

∵∠BEC=∠BED+∠DEC=∠BED+60°;

∴∠ADC=∠BED+60°

在△BDE中，∠BDE=180°-∠DBE-∠BED=180°-66°-∠BED=114°-∠BED

∴∠ADB=360°-∠ADC-∠BDE-∠EDC=360°-（∠BED+60°）-（114°-∠BED）-60°=126°

故答案为：126°