题目内容
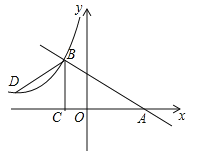
【题目】如图,长方形ABOD的顶点A是函数y=-x-(k+1)的图象与函数y=![]() 在第二象限的图象的交点,B,D两点在坐标轴上,且长方形ABOD的面积为3.
在第二象限的图象的交点,B,D两点在坐标轴上,且长方形ABOD的面积为3.
(1)求两函数的表达式;
(2)求两函数图象的交点A,C的坐标;
(3)若点P是y轴上一动点,且S△APC=5,求点P的坐标.

【答案】(1)反比例函数的表达式为y=-![]() ,一次函数的表达式为y=-x+2(2)点A,C的坐标分别为(-1,3),(3,-1)(3)点P的坐标为(0,
,一次函数的表达式为y=-x+2(2)点A,C的坐标分别为(-1,3),(3,-1)(3)点P的坐标为(0, ![]() )或(0,-
)或(0,-![]() )
)
【解析】试题分析:(1)根据图象所在的象限结合矩形ABOD的面积,就能求出k的值,进而求出两函数的表达式;
(2)将两函数解析式联立消元,求出其解,即得到交点A、C的坐标;
(3),设点P的坐标为(0,m),直线y=-x+2与y轴的交点坐标为M(0,2),根据S△APC=S△AMP+S△CMP=5解答即可.
试题解析:(1)由图象知k<0,由已知条件得|k|=3,
∴k=-3.
∴反比例函数的表达式为y=-![]() ,
,
一次函数的表达式为y=-x+2.
(2)由y=-![]() 与y=-x+2可得,-
与y=-x+2可得,- ![]() =-x+2,
=-x+2,
去分母整理后得x2-2x-3=0,
x2-2x+1-4=0,
(x-1)2=4,
∴x-1=±2,
即x1=-1,x2=3.
∴y1=3,y2=-1.
∴点A,C的坐标分别为(-1,3),(3,-1).
(3)设点P的坐标为(0,m),直线y=-x+2与y轴的交点为M,则M的坐标为(0,2).
∵S△APC=S△AMP+S△CMP=![]() ×PM×(|-1|+|3|)=5,
×PM×(|-1|+|3|)=5,
∴PM=![]() ,即|m-2|=
,即|m-2|=![]() .
.
∴m=![]() 或m=-
或m=-![]() .
.
∴点P的坐标为(0, ![]() )或(0,-
)或(0,-![]() ).
).

练习册系列答案
相关题目