题目内容
【题目】如图,函数y= ![]() 的图象过点A(1,2).
的图象过点A(1,2). 
(1)求该函数的解析式;
(2)过点A分别向x轴和y轴作垂线,垂足为B和C,求四边形ABOC的面积;
(3)求证:过此函数图象上任意一点分别向x轴和y轴作垂线,这两条垂线与两坐标轴所围成矩形的面积为定值.
【答案】
(1)解:∵函数y= ![]() 的图象过点A(1,2),
的图象过点A(1,2),
∴将点A的坐标代入反比例函数解析式,
得2= ![]() ,解得:k=2,
,解得:k=2,
∴反比例函数的解析式为y= ![]()
(2)解:∵点A是反比例函数上一点,
∴矩形ABOC的面积S=ACAB=|xy|=|k|=2
(3)解:设图象上任一点的坐标(x,y),
∴过这点分别向x轴和y轴作垂线,矩形面积为|xy|=|k|=2,
∴矩形的面积为定值.
【解析】(1)将点A的坐标代入反比例函数解析式,即可求出k值;(2)由于点A是反比例函数上一点,矩形ABOC的面积S=|k|.(3)设图象上任一点的坐标(x,y),根据矩形的面积公式,可得出结论.
【考点精析】本题主要考查了比例系数k的几何意义的相关知识点,需要掌握几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积才能正确解答此题.

练习册系列答案
相关题目
【题目】一位射击运动员在10次射击训练中,命中靶的环数如图. 请你根据图表,完成下列问题: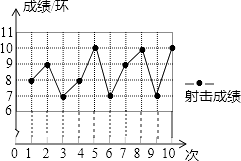
(1)补充完成下面成绩表单的填写:
射击序次 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩/环 | 8 | 10 | 7 | 9 | 10 | 7 | 10 |
(2)求该运动员这10次射击训练的平均成绩.



