��Ŀ����
����Ŀ����ͼ����֪���κ���y= ![]() x2+
x2+ ![]() x��
x�� ![]() ��ͼ����x�ύ�ڵ� A��B���� y ���ڵ� C�������ߵĶ���Ϊ D��
��ͼ����x�ύ�ڵ� A��B���� y ���ڵ� C�������ߵĶ���Ϊ D��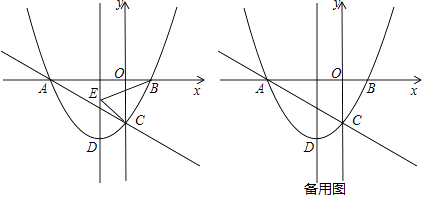
��1���������߶��� D �������Լ�ֱ�� AC �ĺ�������ʽ��
��2���� P ����������һ�㣬�ҵ�P��ֱ�� AC �·����� E �������߶Գ����ϣ�����BCE ���ܳ���Сʱ�����PCE ��������ֵ�Լ���ʱ�� P �����ꣻ
��3���ڣ�2���������£����� P ��ƽ���� AC ��ֱ�߷ֱ�x���ڵ� M���� y ���ڵ�N����������y= ![]() x2+
x2+ ![]() x��
x�� ![]() �ضԳ�������ƽ�ƣ�ƽ�ƺ������ߵĶ���Ϊ D'����ƽ�ƵĹ����У��Ƿ���ڵ� D'��ʹ�õ� D'��M��N ���㹹�ɵ�������Ϊֱ�������Σ������ڣ�ֱ��д���� D'�����ꣻ�������ڣ���˵�����ɣ�
�ضԳ�������ƽ�ƣ�ƽ�ƺ������ߵĶ���Ϊ D'����ƽ�ƵĹ����У��Ƿ���ڵ� D'��ʹ�õ� D'��M��N ���㹹�ɵ�������Ϊֱ�������Σ������ڣ�ֱ��д���� D'�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1���⣺y= ![]() x2+
x2+ ![]() x��
x�� ![]() =
= ![]() ��x+1��2��
��x+1��2�� ![]() ������D����������1����
������D����������1���� ![]() ����
����
��y=0ʱ�� ![]() x2+
x2+ ![]() x��
x�� ![]() =0�����x1=��3��x2=1��
=0�����x1=��3��x2=1��
��A����3��0����B��1��0����
��x=0ʱ��y=�� ![]() ��
��
��C��0���� ![]() ����
����
��ֱ��AC�Ľ���ʽΪy=�� ![]() x��
x�� ![]()
��2���⣺�ߡ�CPE���ܳ�ΪBC+CE+BE������BC�ij��ǹ̶��ģ�
���ܳ�ȡ����Сֵ����BE+CEȡ����Сֵ��
�ߵ�E�������߶Գ�����һ�㣬
��BE=AE��
��BE+CE=AE+CE��
��BE+CE����Сֵ��AC����E��AC��Գ���Ľ��㣮
���E����1���� ![]() ����
����
�ߵ�P����������x���·�һ�㣬���PΪ��t�� ![]() t2+
t2+ ![]() t��
t�� ![]() ������
������ ![]() t2+
t2+ ![]() t��
t�� ![]() ��0��
��0��
����P��QP��x�ύֱ��AC�ڵ�Q����Q����Ϊ��t���� ![]() t��
t�� ![]() ����
����
����p�ڶԳ������ʱ��S��PCE=S��PCQ��S��PEQ= ![]() PQ��0��t����
PQ��0��t���� ![]() PQ����1��t��=
PQ����1��t��= ![]() PQ��
PQ��
����P�ڶԳ�����Ҳ�ʱ��S��PCE=S��PCQ+S��PEQ= ![]() PQ��0��t��+
PQ��0��t��+ ![]() PQ[t������1��]=
PQ[t������1��]= ![]() PQ��
PQ��
��PQ=���� ![]() t��
t�� ![]() ������
������ ![]() t2+
t2+ ![]() t��
t�� ![]() ��=��
��=�� ![]() t2��
t2�� ![]() t��
t��
��S��PCE= ![]() PQ=��
PQ=�� ![]() t2��
t2�� ![]() t=��
t=�� ![]() ��t+
��t+ ![]() ��2+
��2+ ![]() ��
��
��t=�� ![]() ʱ����PEC�����������ֵ��
ʱ����PEC�����������ֵ�� ![]() ����ʱ����P������Ϊ����
����ʱ����P������Ϊ���� ![]() ����
���� ![]() ��
��
��3���⣺������P��ƽ����AC��ֱ��MN�Ľ���ʽΪy=�� ![]() x��
x�� ![]() ��
��
��x=0ʱ��y=�� ![]() ����N��0����
����N��0���� ![]() ������y=0ʱ��x=��
������y=0ʱ��x=�� ![]() ����M����
����M���� ![]() ��0����
��0����
���D�����������1��d������MN2=���� ![]() ��2+����
��2+���� ![]() ��2=
��2= ![]() ��MD��2=[��
��MD��2=[�� ![]() ������1��]2+d2=
������1��]2+d2= ![]() +d2��ND��2=����1��2+����
+d2��ND��2=����1��2+���� ![]() ��d��2=d2+
��d��2=d2+ ![]() d+
d+ ![]() ��
��
����MD��N=90��ʱ��MD��2+ND��2=MN2���� ![]() +d2+d2+
+d2+d2+ ![]() d+
d+ ![]() =
= ![]() ��
��
��������4d2+7 ![]() d��17=0�����d1=
d��17=0�����d1= ![]() ��d2=
��d2= ![]() ��
��
����NMD��=90��ʱ��MD��2=ND��2+MN2���� ![]() +d2=d2+
+d2=d2+ ![]() d+
d+ ![]() +
+ ![]() ��
��
���� ![]() d=��
d=�� ![]() �����d=��
�����d=�� ![]() ��
��
����NMD�䩁90��ʱ��ND��2=MD��2+MN2����d2+ ![]() d+
d+ ![]() =
= ![]() +d2+
+d2+ ![]() ��
��
���� ![]() d=
d= ![]() �����d=
�����d= ![]() ��
��
����ڵ� D'��ʹ�õ� D'��M��N ���㹹�ɵ�������Ϊֱ�������Σ�D��������Ϊ����1�� ![]() ������1��
������1�� ![]() ��������1��
��������1�� ![]() ������1
������1 ![]() ��
��
����������1�������䷽������ɶ���ʽ������������ꣻ��2����BCE ���ܳ���С����CE+BE��С���ɶԳƷ�����õ�E��AC��Գ���Ľ��㴦ʱ����BCE ���ܳ���С����PCE ��������ֵ�����ú���˼�룬���P�ĺ�����Ϊt������������t�Ĵ���ʽ��ʾ������x�ᴹ�ߣ��ѡ�PCE �ָ�Ϊ��������ֱ�ߵ������Σ�������������ĺ�������ɶ���ʽ�����ֵ����3��D'��M��N ���㹹�ɵ�������Ϊֱ����������������ۣ���MD��N=90����NMD��=90����NMD�䩁90�㣬���ù��ɶ����г�����.

����Ŀ��ij������������ÿ̨���۷ֱ�Ϊ2000Ԫ��1700Ԫ��![]() ��
��![]() �����ͺŵĿյ�������ǽ����ܵ����������
�����ͺŵĿյ�������ǽ����ܵ����������
����ʱ�� | �������� | ���ۿ� | |
|
| ||
��һ�� | 4̨ | 5̨ | 20500Ԫ |
�ڶ��� | 5̨ | 10̨ | 33500Ԫ |
��1����![]() ��
��![]() �����ͺŵĿյ������۵��ۣ�
�����ͺŵĿյ������۵��ۣ�
��2��������ܵ���������
����Ŀ��������������ѧ�Ļ���������Ϊ�˽�һ���˽�ѧ���ļ����������2020����ѧ��ʦ�Ƕ�ij�ο����е�19�������ĵ÷���������˵��飬�ֱַ��A��B�����������ȡ10��ѧ���ijɼ����£�
A��10��ѧ���ijɼ����������ͳ��ͼ������ͼ��

B��10��ѧ���ijɼ�����λ���֣��ֱ�Ϊ��9��8��9��10��9��7��9��8��10��8
������ʦ������ȡѧ���ɼ���������������õ������±����ݣ�
A�� | B�� | |
ƽ���� | 8.3 | a |
��� | b | 9 |
���� | 8��10 | c |
���� | 4 | 3 |
���� | 1.81 | 0.81 |
����������Ϣ������������⣮
��1����ȫ����ͳ��ͼ��
��2��ֱ��д������a��b��c��ֵ��a���� ����b���� ����c���� ����
��3�������������ݣ�����ΪA��B�������ĸ�����������յø��ã���˵�����ɣ�д�������������ɣ����� ����
��4����9�ּ�9������Ϊ���㣬��A�55�ˣ���A�����������Ĵ�Լ�ж����ˣ�