题目内容
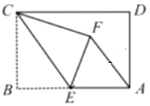
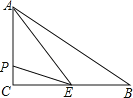
【题目】把△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得到△AB′C′,即如图,∠BAB′=θ, ![]() =
= ![]() =
= ![]() =n,我们将这种变换记为[θ,n].△ABC中,AB=AC,∠BAC=36°,BC=1,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB′C′为平行四边形,那么θ= , n= .
=n,我们将这种变换记为[θ,n].△ABC中,AB=AC,∠BAC=36°,BC=1,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB′C′为平行四边形,那么θ= , n= . 
【答案】72°;![]()
【解析】解:∵四边形ABB′C′是平行四边形,
∴AC′∥BB′,
又∵∠BAC=36°,
∴θ=∠CAC′=∠ACB=72°,
∴∠C′AB′=∠ABB′=∠BAC=36°,而∠B=∠B,
∴△ABC∽△B′BA,
∴AB2=CBB′B=CB(BC+CB′),而CB′=AC=AB=B′C′,BC=1,
∴AB2=1(1+AB),
∴AB= ![]() ,
,
∵AB>0,
∴n= ![]() =
= ![]() .
.
所以答案是:72°, ![]() .
.
【考点精析】本题主要考查了等腰三角形的性质和平行四边形的性质的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分才能正确解答此题.

【题目】计算能力是数学的基本能力,为了进一步了解学生的计算情况,初2020级数学老师们对某次考试中第19题计算题的得分情况进行了调查,现分别从A、B两班随机各抽取10名学生的成绩如下:
A班10名学生的成绩绘成了条形统计图,如下图,

B班10名学生的成绩(单位:分)分别为:9,8,9,10,9,7,9,8,10,8
经过老师对所抽取学生成绩的整理与分析,得到了如下表数据:
A班 | B班 | |
平均数 | 8.3 | a |
中位数 | b | 9 |
众数 | 8或10 | c |
极差 | 4 | 3 |
方差 | 1.81 | 0.81 |
根据以上信息,解答下列问题.
(1)补全条形统计图;
(2)直接写出表中a,b,c的值:a= ,b= ,c= ;
(3)根据以上数据,你认为A、B两个班哪个班计算题掌握得更好?请说明理由(写出其中两条即可): .
(4)若9分及9分以上为优秀,若A班共55人,则A班计算题优秀的大约有多少人?