题目内容
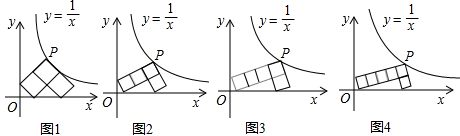
如图1~4所示,每个图中的“7”字形是由若干个边长相等的正方形拼接而成,“7”字形的一个顶点P落在反比例函数y= 的图象上,另“7”字形有两个顶点落在x轴上,一个顶点落在y轴上.
的图象上,另“7”字形有两个顶点落在x轴上,一个顶点落在y轴上.
(1)图1中的每一个小正方形的面积是______;
(2)按照图1→图2→图→图4→…这样的规律拼接下去,第n个图形中每一个小正方形的面积是______.(用含n的代数式表示)
解: (1)作PA⊥y轴于A,图中的“7”字形与坐标轴的交点分别为B、C、D,如图1,
(1)作PA⊥y轴于A,图中的“7”字形与坐标轴的交点分别为B、C、D,如图1,
设每一个小正方形的边长为a,
易证得Rt△ECD∽Rt△OBC∽Rt△APB,
∴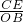 =
=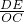 ,
,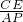 =
= ,
,
∴ =
= =
=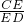 =
= =1,
=1,
在RtOBC中,BC=a,
∵OB2+OC2=BC2=a2,OB=OC,
∴OB=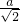 ,
,
在Rt△ABP中,PB=2a,
∵AB2+AP2=BP2=4a2,AB=AP,
∴AB=AP=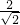 a,
a,
∴OA=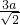 ,
,
∴P点坐标为(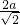 ,
,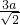 ),
),
∴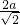 •
•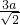 =1,
=1,
∴a2= ;
;
(2)如图2,同样得到Rt△ECD∽Rt△OBC∽Rt△APB,
∴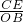 =
=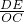 ,
,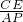 =
= ,
,
∴ =
= =
=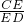 =
= =2,
=2,
在RtOBC中,BC=a,
∵OB2+OC2=BC2=a2,OB=2OC,
∴OB=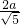 ,
,
在Rt△ABP中,PB=3a,
∵AB2+AP2=BP2=9a2,AB=2AP,
∴AB=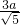 ,AP=
,AP=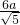
∴OA=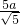 ,
,
∴P点坐标为(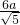 ,
,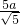 ),
),
∴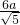 •
•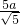 =1,
=1,
∴a2= ;
;
如图3,易证得Rt△ECD∽Rt△OBC∽Rt△APB,
∴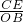 =
=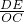 ,
,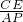 =
= ,
,
∴ =
= =
=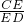 =
=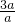 =3,
=3,
同理可得a2=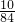 ;
;
如图4,易证得Rt△ECD∽Rt△OBC∽Rt△APB,
∴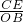 =
=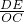 ,
,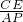 =
= ,
,
∴ =
= =
=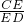 =
=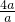 =4,
=4,
同理可得a2=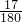 ;
;
∵第1个图每一个小正方形的面积= =
=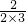 =
=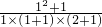 ;
;
第2个图每一个小正方形的面积= =
=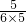 =
=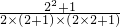 ;
;
第3个图每一个小正方形的面积=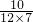 =
=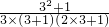 ;
;
第4个图每一个小正方形的面积=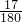 =
=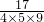 =
=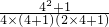 ,
,
∴第n个图每一个小正方形的面积=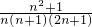 .
.
故答案为(1) ;(2)
;(2)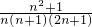 .
.
分析:(1)作PA⊥y轴于A,图中的“7”字形与坐标轴的交点分别为B、C、D,如图1,设每一个小正方形的边长为a,证得Rt△ECD∽Rt△OBC∽Rt△APB,利用相似比得到 =
= =
=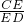 =
= =1,再分别在在RtOBC和Rt△ABP中,利用勾股定理得到OB=
=1,再分别在在RtOBC和Rt△ABP中,利用勾股定理得到OB=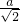 ,AB=AP=
,AB=AP=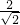 a,则P点坐标为(
a,则P点坐标为(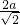 ,
,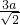 ),然后把P点坐标代入反比例函数解析式得到a2=
),然后把P点坐标代入反比例函数解析式得到a2= ;
;
(2)对于如图2、图3、图4利用同样的方法可得到每一个小正方形的面积,然后把计算的结果进行变形,观察其中的规律,可发现第n个图每一个小正方形的面积=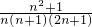 .
.
点评:本题考查了反比例函数的综合题:反比例函数图象的点的坐标满足其函数解析式;熟练运用正方形的性质、相似三角形的相似比和勾股定理进行计算.
 (1)作PA⊥y轴于A,图中的“7”字形与坐标轴的交点分别为B、C、D,如图1,
(1)作PA⊥y轴于A,图中的“7”字形与坐标轴的交点分别为B、C、D,如图1,设每一个小正方形的边长为a,
易证得Rt△ECD∽Rt△OBC∽Rt△APB,
∴
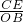 =
=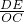 ,
,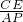 =
= ,
,∴
 =
= =
=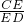 =
= =1,
=1,在RtOBC中,BC=a,
∵OB2+OC2=BC2=a2,OB=OC,
∴OB=
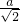 ,
,在Rt△ABP中,PB=2a,
∵AB2+AP2=BP2=4a2,AB=AP,
∴AB=AP=
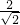 a,
a,∴OA=
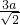 ,
,∴P点坐标为(
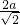 ,
,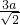 ),
),∴
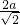 •
•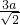 =1,
=1,∴a2=
 ;
;(2)如图2,同样得到Rt△ECD∽Rt△OBC∽Rt△APB,
∴
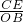 =
=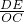 ,
,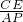 =
= ,
,∴
 =
= =
=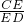 =
= =2,
=2,在RtOBC中,BC=a,
∵OB2+OC2=BC2=a2,OB=2OC,
∴OB=
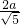 ,
,在Rt△ABP中,PB=3a,
∵AB2+AP2=BP2=9a2,AB=2AP,
∴AB=
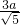 ,AP=
,AP=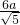
∴OA=
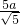 ,
,∴P点坐标为(
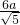 ,
,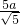 ),
),∴
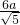 •
•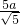 =1,
=1,∴a2=
 ;
;如图3,易证得Rt△ECD∽Rt△OBC∽Rt△APB,
∴
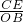 =
=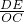 ,
,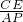 =
= ,
,∴
 =
= =
=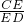 =
=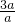 =3,
=3,同理可得a2=
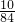 ;
;如图4,易证得Rt△ECD∽Rt△OBC∽Rt△APB,
∴
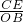 =
=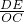 ,
,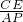 =
= ,
,∴
 =
= =
=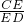 =
=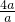 =4,
=4,同理可得a2=
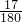 ;
;∵第1个图每一个小正方形的面积=
 =
=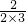 =
=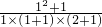 ;
;第2个图每一个小正方形的面积=
 =
=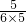 =
=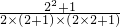 ;
;第3个图每一个小正方形的面积=
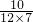 =
=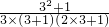 ;
;第4个图每一个小正方形的面积=
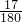 =
=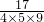 =
=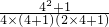 ,
,∴第n个图每一个小正方形的面积=
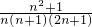 .
.故答案为(1)
 ;(2)
;(2)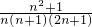 .
.分析:(1)作PA⊥y轴于A,图中的“7”字形与坐标轴的交点分别为B、C、D,如图1,设每一个小正方形的边长为a,证得Rt△ECD∽Rt△OBC∽Rt△APB,利用相似比得到
 =
= =
=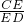 =
= =1,再分别在在RtOBC和Rt△ABP中,利用勾股定理得到OB=
=1,再分别在在RtOBC和Rt△ABP中,利用勾股定理得到OB=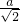 ,AB=AP=
,AB=AP=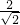 a,则P点坐标为(
a,则P点坐标为(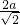 ,
,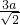 ),然后把P点坐标代入反比例函数解析式得到a2=
),然后把P点坐标代入反比例函数解析式得到a2= ;
;(2)对于如图2、图3、图4利用同样的方法可得到每一个小正方形的面积,然后把计算的结果进行变形,观察其中的规律,可发现第n个图每一个小正方形的面积=
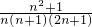 .
.点评:本题考查了反比例函数的综合题:反比例函数图象的点的坐标满足其函数解析式;熟练运用正方形的性质、相似三角形的相似比和勾股定理进行计算.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


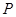 落在反比例函数
落在反比例函数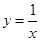 的图像上,另“7”字形有两个顶点落在
的图像上,另“7”字形有两个顶点落在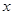 轴上,一个顶点落在
轴上,一个顶点落在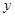 轴上.
轴上.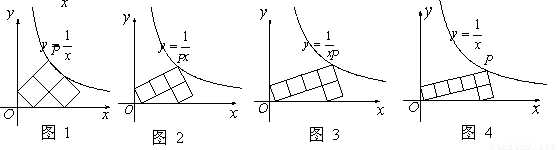
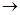 图2
图2 这样的规律拼接下去,第
这样的规律拼接下去,第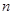 个图形中每一个小正方形的面积是
.(用含
个图形中每一个小正方形的面积是
.(用含