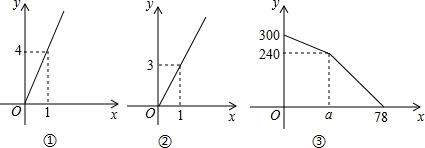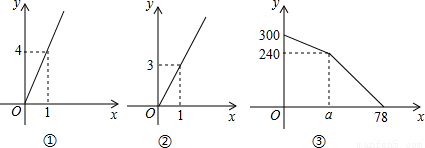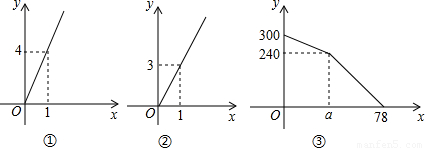题目内容
某车站客流量大,旅客往往需长时间排队等候购票,经调查统计发现,每天开始售票时,约有300名旅客排队等候购票,同时有新的旅客不断进入售票厅排队等候购票,新增购票人数y(人)与售票时间 x(分)的函数关系如图(1)所示;每个售票窗口售票数y(人)与售票时间x(分)的函数关系如图(2)所示,某天售票厅排队等候购票的人数y(人)与售票时间x(分)的函数关系如图(3)所示,已知售票的前a分钟开放了两个售票窗口。
(1)求a的值;
(2)求售票到第60分钟时,售票厅排队等候购票的旅客人数;
(3)该车站在学习实践科学发展观的活动中,本着“以 人为本,方便旅客”的宗旨,决定增设售票窗口.若 要在开始售票后半小时内让所有排队购票的旅客都能购到票,以便后来到站的旅客能随到随购,请你帮助计算,至少需同时开放几个售票窗口?
(1)求a的值;
(2)求售票到第60分钟时,售票厅排队等候购票的旅客人数;
(3)该车站在学习实践科学发展观的活动中,本着“以 人为本,方便旅客”的宗旨,决定增设售票窗口.若 要在开始售票后半小时内让所有排队购票的旅客都能购到票,以便后来到站的旅客能随到随购,请你帮助计算,至少需同时开放几个售票窗口?
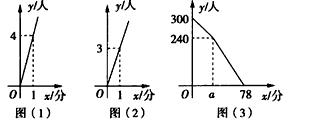
解:(1)由题图(1)、(2)可知,每分钟新增购票人数为4人,每个售票窗口每分钟售票3人,则300+4×a-3×2×a=240,
解这个方程,得 a=30,
即a的值为30;
(2)设第30 ~78分钟时,售票厅排队等候购票人数y与售票时间x的函数关系式为y=kx+b,
所以可得30k+b=240,78k+b=0,
解得k=-5,b=390,
∴y=-5x+390,
当x=60时,y=-5×60+390=90(人),
因此,到第60分钟时,售票厅排队等候购票的旅客有90人;
(3)设至少同时开放n个售票窗口,依题意得:
300+30×4≤30×3×n,
解这个不等式,得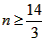 ,
,
因此至少同时开放5个售票窗口。
解这个方程,得 a=30,
即a的值为30;
(2)设第30 ~78分钟时,售票厅排队等候购票人数y与售票时间x的函数关系式为y=kx+b,
所以可得30k+b=240,78k+b=0,
解得k=-5,b=390,
∴y=-5x+390,
当x=60时,y=-5×60+390=90(人),
因此,到第60分钟时,售票厅排队等候购票的旅客有90人;
(3)设至少同时开放n个售票窗口,依题意得:
300+30×4≤30×3×n,
解这个不等式,得
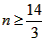 ,
, 因此至少同时开放5个售票窗口。

练习册系列答案
相关题目