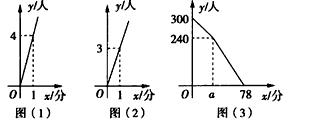
��Ŀ����
��ͼ1��4��ʾ��ÿ��ͼ�еġ�7�������������ɸ��߳���ȵ�������ƴ�Ӷ��ɣ���7�����ε�һ������P���ڷ���������y=
��ͼ���ϣ�����7��������������������x���ϣ�һ����������y���ϣ�
��1��ͼ1�е�ÿһ��С�����ε������
��
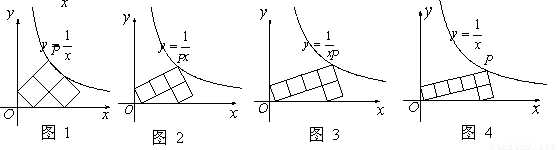
��2������ͼ1��ͼ2��ͼ��ͼ4���������Ĺ���ƴ����ȥ����n��ͼ����ÿһ��С�����ε������
�����ú�n�Ĵ���ʽ��ʾ��

| 1 |
| x |
��1��ͼ1�е�ÿһ��С�����ε������
| 1 |
| 3 |
| 1 |
| 3 |
��2������ͼ1��ͼ2��ͼ��ͼ4���������Ĺ���ƴ����ȥ����n��ͼ����ÿһ��С�����ε������
| n2+1 |
| n(n+1)(2n+1) |
| n2+1 |
| n(n+1)(2n+1) |

��������1����PA��y����A��ͼ�еġ�7��������������Ľ���ֱ�ΪB��C��D����ͼ1����ÿһ��С�����εı߳�Ϊa��֤��Rt��ECD��Rt��OBC��Rt��APB���������Ʊȵõ�
=
=
=
=1���ٷֱ�����RtOBC��Rt��ABP�У����ù��ɶ����õ�OB=
��AB=AP=
a����P��������
��
����Ȼ���P��������뷴������������ʽ�õ�a2=
��
��2��������ͼ2��ͼ3��ͼ4����ͬ���ķ����ɵõ�ÿһ��С�����ε������Ȼ��Ѽ���Ľ�����б��Σ��۲����еĹ��ɣ��ɷ��ֵ�n��ͼÿһ��С�����ε����=
��
| OB |
| OC |
| AP |
| AB |
| CE |
| ED |
| a |
| a |
| a | ||
|
| 2 | ||
|
| 2a | ||
|
| 3a | ||
|
| 1 |
| 3 |
��2��������ͼ2��ͼ3��ͼ4����ͬ���ķ����ɵõ�ÿһ��С�����ε������Ȼ��Ѽ���Ľ�����б��Σ��۲����еĹ��ɣ��ɷ��ֵ�n��ͼÿһ��С�����ε����=
| n2+1 |
| n(n+1)(2n+1) |
����⣺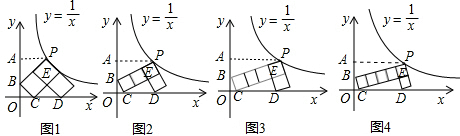 ��1����PA��y����A��ͼ�еġ�7��������������Ľ���ֱ�ΪB��C��D����ͼ1��
��1����PA��y����A��ͼ�еġ�7��������������Ľ���ֱ�ΪB��C��D����ͼ1��
��ÿһ��С�����εı߳�Ϊa��
��֤��Rt��ECD��Rt��OBC��Rt��APB��
��
=
��
=
��
��
=
=
=
=1��
��RtOBC��BC=a��
��OB2+OC2=BC2=a2��OB=OC��
��OB=
��
��Rt��ABP��PB=2a��
��AB2+AP2=BP2=4a2��AB=AP��
��AB=AP=
a��
��OA=
��
��P��������
��
����
��
•
=1��
��a2=
��
��2����ͼ2��ͬ���õ�Rt��ECD��Rt��OBC��Rt��APB��
��
=
��
=
��
��
=
=
=
=2��
��RtOBC��BC=a��
��OB2+OC2=BC2=a2��OB=2OC��
��OB=
��
��Rt��ABP��PB=3a��
��AB2+AP2=BP2=9a2��AB=2AP��
��AB=
��AP=
��OA=
��
��P��������
��
����
��
•
=1��
��a2=
��
��ͼ3����֤��Rt��ECD��Rt��OBC��Rt��APB��
��
=
��
=
��
��
=
=
=
=3��
ͬ���ɵ�a2=
��
��ͼ4����֤��Rt��ECD��Rt��OBC��Rt��APB��
��
=
��
=
��
��
=
=
=
=4��
ͬ���ɵ�a2=
��
�ߵ�1��ͼÿһ��С�����ε����=
=
=
��
��2��ͼÿһ��С�����ε����=
=
=
��
��3��ͼÿһ��С�����ε����=
=
��
��4��ͼÿһ��С�����ε����=
=
=
��
���n��ͼÿһ��С�����ε����=
��
�ʴ�Ϊ��1��
����2��
��
 ��1����PA��y����A��ͼ�еġ�7��������������Ľ���ֱ�ΪB��C��D����ͼ1��
��1����PA��y����A��ͼ�еġ�7��������������Ľ���ֱ�ΪB��C��D����ͼ1����ÿһ��С�����εı߳�Ϊa��
��֤��Rt��ECD��Rt��OBC��Rt��APB��
��
| CE |
| OB |
| DE |
| OC |
| CE |
| AP |
| DE |
| AB |
��
| OB |
| OC |
| AP |
| AB |
| CE |
| ED |
| a |
| a |
��RtOBC��BC=a��
��OB2+OC2=BC2=a2��OB=OC��
��OB=
| a | ||
|
��Rt��ABP��PB=2a��
��AB2+AP2=BP2=4a2��AB=AP��
��AB=AP=
| 2 | ||
|
��OA=
| 3a | ||
|
��P��������
| 2a | ||
|
| 3a | ||
|
��
| 2a | ||
|
| 3a | ||
|
��a2=
| 1 |
| 3 |
��2����ͼ2��ͬ���õ�Rt��ECD��Rt��OBC��Rt��APB��
��
| CE |
| OB |
| DE |
| OC |
| CE |
| AP |
| DE |
| AB |
��
| OB |
| OC |
| AP |
| AB |
| CE |
| ED |
| 2a |
| a |
��RtOBC��BC=a��
��OB2+OC2=BC2=a2��OB=2OC��
��OB=
| 2a | ||
|
��Rt��ABP��PB=3a��
��AB2+AP2=BP2=9a2��AB=2AP��
��AB=
| 3a | ||
|
| 6a | ||
|
��OA=
| 5a | ||
|
��P��������
| 6a | ||
|
| 5a | ||
|
��
| 6a | ||
|
| 5a | ||
|
��a2=
| 5 |
| 30 |
��ͼ3����֤��Rt��ECD��Rt��OBC��Rt��APB��
��
| CE |
| OB |
| DE |
| OC |
| CE |
| AP |
| DE |
| AB |
��
| OB |
| OC |
| AP |
| AB |
| CE |
| ED |
| 3a |
| a |
ͬ���ɵ�a2=
| 10 |
| 84 |
��ͼ4����֤��Rt��ECD��Rt��OBC��Rt��APB��
��
| CE |
| OB |
| DE |
| OC |
| CE |
| AP |
| DE |
| AB |
��
| OB |
| OC |
| AP |
| AB |
| CE |
| ED |
| 4a |
| a |
ͬ���ɵ�a2=
| 17 |
| 180 |
�ߵ�1��ͼÿһ��С�����ε����=
| 1 |
| 3 |
| 2 |
| 2��3 |
| 12+1 |
| 1��(1+1)��(2+1) |
��2��ͼÿһ��С�����ε����=
| 5 |
| 30 |
| 5 |
| 6��5 |
| 22+1 |
| 2��(2+1)��(2��2+1) |
��3��ͼÿһ��С�����ε����=
| 10 |
| 12��7 |
| 32+1 |
| 3��(3+1)(2��3+1) |
��4��ͼÿһ��С�����ε����=
| 17 |
| 180 |
| 17 |
| 4��5��9 |
| 42+1 |
| 4��(4+1)(2��4+1) |
���n��ͼÿһ��С�����ε����=
| n2+1 |
| n(n+1)(2n+1) |
�ʴ�Ϊ��1��
| 1 |
| 3 |
| n2+1 |
| n(n+1)(2n+1) |
���������⿼���˷������������ۺ��⣺����������ͼ��ĵ�����������亯������ʽ���������������ε����ʡ����������ε����ƱȺ��ɶ������м��㣮

��ϰ��ϵ�д�
�����Ŀ

 ��ͼ���ϣ�����7��������������������x���ϣ�һ����������y���ϣ�
��ͼ���ϣ�����7��������������������x���ϣ�һ����������y���ϣ�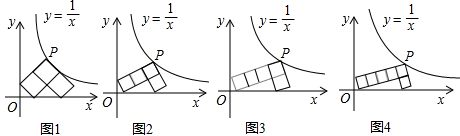
 ���ڷ���������
���ڷ���������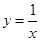 ��ͼ���ϣ�����7��������������������
��ͼ���ϣ�����7��������������������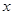 ���ϣ�һ����������
���ϣ�һ����������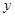 ����.
����.
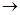 ͼ2
ͼ2 �����Ĺ���ƴ����ȥ����
�����Ĺ���ƴ����ȥ����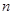 ��ͼ����ÿһ��С�����ε������
.���ú�
��ͼ����ÿһ��С�����ε������
.���ú�