题目内容
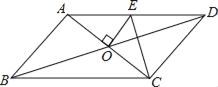
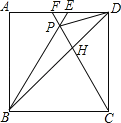
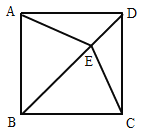
【题目】如图，在正方形ABCD中，E是对角线BD上一点，连接AE，CE．
（1）求证：AE=CE；
（2）若BC=
，BE=6，求tan∠BAE的值.
【答案】(1)见解析;(2)3.
【解析】
（1）通过SAS证明△ADE≌△CDE即可得；
（2）过点E作AB的垂线相交于点P，由△BPE为等腰直角三角形求出BP=EP=
，从而得到AP，在直角△APE中由正切的定义求解即可.
解：（1）证明：在正方形ABCD中 AD=CD, ∠ADE=∠CDE=45°
在△ADE和△CDE中
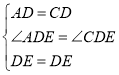
∴△ADE≌△CDE (SAS)，
∴AE=CE
(2)如图所示，过点E作AB的垂线相交于点P，
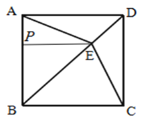
易得 △BPE为等腰直角三角形，
∵BE=6，由勾股定理可知BP=EP=
而AB=BC=
∴AP=AB-BP=
∴
.
【题目】为拓宽学生视野，我市某中学决定组织部分师生去庐山西海开展研学旅行活动，在参加此次活动的师生中，若每位老师带17个学生，还剩12个学生没人带；若每位老师带18个学生，就有一位老师少带4个学生．为了安全，既要保证所有师生都有车坐，又要保证每辆客车上至少要有2名老师．现有甲、乙两种大客车，它们的载客量和租金如表所示．
甲种客车 | 乙种客车 | |
载客量/（人/辆） | 30 | 42 |
租金/（元/辆） | 300 | 400 |
（1）参加此次研学旅行活动的老师和学生各有多少人？租用客车总数为多少辆？
（2）设租用x辆乙种客车，租车总费用为w元，请写出w与x之间的函数关系式；
（3）在（2）的条件下，学校计划此次研学旅行活动的租车总费用不超过3100元，租用乙种客车不少5辆，你能得出哪几种不同的租车方案？其中哪种租车方案最省钱？请说明理由．
【题目】2019年永州市初中体育水平测试进行改革，增加了自选项目，学生可以从篮球运球、足球运球、排球向上垫球三项中必须选一项，另外从一分钟跳绳、仰卧起坐（女）或引体向上（男）、原地正面掷实心球、立定跳远中必须选一项．现对永州市某校的选考项目情况进行调查，对调查结果进行了分析统计并制作了两幅统计图：
项目 | 篮球 | 足球 | 排球 | |||
性别 | 男 | 女 | 男 | 女 | 男 | 女 |
人数 | 30 | 10 | 24 | 12 | 6 | 28 |
平均得分 | 8 | 7 | 8.5 | 6 | 9 | 10 |
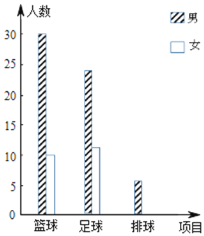
（1）补全条形统计图；
（2）求抽查的这些男生的体育测试平均分；
（3）若该校准备从这次体育测试成绩好的学生中选出10名参加全市运动会．现在有19名学生报名，小明是这19名同学之一，小明在知道自己这次成绩后还需知道这19名学生成绩的______，就能知道自己能不能参加市运动会．
A．平均数B．众数C．中位数D．方差
