题目内容
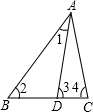
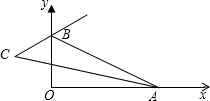
如图，在平面直角坐标系，点A、B分别是x轴正半轴、y轴正半轴上的动点，∠OAB的内角平分线与∠OBA的外角平分线所在直线交于点C，则∠ACB的度数为______．
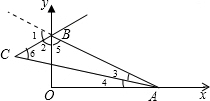
∵BC是∠OBA的外角平分线，
∴∠1+∠2=∠AOB+∠3+∠4，即∠1+∠2=90°+∠3+∠4，
∠1=∠2；
又∵AC是∠OAB的内角平分线，
∴∠3=∠4；
∴∠1=45°+∠3，
∴∠1-∠3=45°；
在△ACB中，
∠ACB=180°-∠3-∠2-∠5，
又∠1+∠2+∠5=180°，
∴∠ACB=∠1+∠2+∠5-∠3-∠2-∠5=∠1-∠3=45°，即∠ACB=45°；
故答案为：45°．
∴∠1+∠2=∠AOB+∠3+∠4，即∠1+∠2=90°+∠3+∠4，
∠1=∠2；
又∵AC是∠OAB的内角平分线，
∴∠3=∠4；
∴∠1=45°+∠3，
∴∠1-∠3=45°；
在△ACB中，
∠ACB=180°-∠3-∠2-∠5，
又∠1+∠2+∠5=180°，
∴∠ACB=∠1+∠2+∠5-∠3-∠2-∠5=∠1-∠3=45°，即∠ACB=45°；
故答案为：45°．
练习册系列答案
相关题目
