题目内容
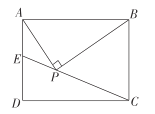
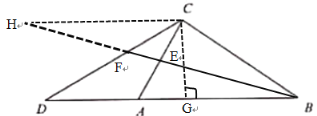
【题目】如图,已知在![]() 中,∠ACB=90°,
中,∠ACB=90°,![]() ,延长边BA至点D,使AD=AC,联结CD.
,延长边BA至点D,使AD=AC,联结CD.
(1)求∠D的正切值;
(2)取边AC的中点E,联结BE并延长交边CD于点F,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)过点C作CG⊥BD于G,根据已知三角函数值,设出参数表示出各边长,可求出CE,DE,进而可得出∠D的正切值.
(2)延长BF至H,使EH=BE,连接CH,则CH∥BD,![]() =
=![]() ,求出
,求出![]() 的值即可.
的值即可.
过点C作CG⊥BD于G,
∵![]() ,∴设AC=3a,则AB=5a,
,∴设AC=3a,则AB=5a,
易得∠ABC=∠ACG,∴sin∠ACG=![]() ,
,
∴AG=AC·sin∠ACG=![]() ,∴CG=
,∴CG=![]()
又AD=AC=3a,∴DG=AD+AG=![]()
∴tanD=![]() ,即∠D的正切值为
,即∠D的正切值为![]() .
.
延长BF至H,使EH=BE,连接CH,由CE=AE,则CH∥BD,
∴![]() =
=![]() ,△CEH≌△AEB,
,△CEH≌△AEB,
∴CH=AB=5a,
又BD=AD+AB=AE+AB=3a+5a=8a,
∴![]() =
=![]() =
=![]() .
.

练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目