题目内容

附加题
①观察下列各式：31=3，32=9，33=27，34=81，35=243，36=729…，则32008的末尾数字是
 
；
②规定一种新运算“*”，对于任意实数a和b，有a*b=a÷b+1，则（6x3y-3xy2）*3xy=
 
；
③如图，在5×5的正方形网格中，每个小正方形都为1，请在给定网格中按下列要求画出图形：
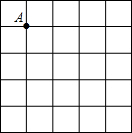精英家教网（1）从点A出发画一条线段AB，使它的另一端点B在格点（即小正方形的顶点）上，且长度为
5
；
（2）在图中正方形网格上画出格点四边形，使四边形的边长分别为
5
，
13
，
2
，
10
，并求出这个四边形的面积．
分析：①观察可发现末尾数字为3，9，7，1，且不断重复出现，据此解题．
②因为a*b=a÷b+1，则（6x3y-3xy2）*3xy=（6x3y-3xy3）÷3xy+1，然后化简即可．
③（1）
5
是直角边长为1，2的直角三角形的斜边；
（2）
2
是直角边长为1，1的直角三角形的斜边；
5
是直角边长为1，2的直角三角形的斜边；
10
是直角边长为1，3的直角三角形的斜边；
13
是直角边长为2，3的直角三角形的斜边．
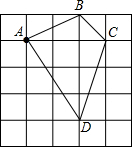解答：精英家教网解：①观察下列各式：31=3，32=9，33=27，34=81，35=243，36=729，
则32008的末尾数字是1；

②（6x3y-3xy2）*3xy=（6x3y-3xy3）÷3xy+1=2x2-y2+1，

③如图，
四边形ABCD的面积为
1
2
×3×1+
1
2
×3×3=6．
点评：解此类问题要注意观察总结规律，提高综合归纳的能力．解决本题的关键是找到所求的无理数是直角边长为哪两个有理数的直角三角形的斜边长．
练习册系列答案
相关题目
附加题阅读、理解和探索
（1）观察下列各式：①
1
1×2
=1-
1
2
；②
1
2×3
=
1
2
-
1
3
；③
1
3×4
=
1
3
-
1
4
；…用你发现的规律写出：第④个式子是（
 
），第n个式子是（
 
）；
（2）利用（1）中的规律，计算：
1
1×2
+
1
2×3
+
1
3×4
+…+
1
9×10
；
（3）应用以上规律化简：
1
n(n+1)
+
1
(n+1)(n+2)
+
1
(n+2)(n+3)
+…+
1
(n+2008)(n+2009)
；
（4）观察按规律排列一组数：
1
3
，
1
15
，
1
35
，…，猜想第n个数是什么（请用含n的式子表达）把它填入求这组数的前n项和：
1
3
+
1
15
+
1
35
+…+（
 
）中的括号内，并把这个和式化简．
附加题：
观察下列各式及其化简过程：
3+2
2
=
(
2
)2+
2×1
+12
=
(+1)2
=
2
+1；
5-2
6
=
(
3
)2-2
3×2
+(
2
)2
=
3
-
2
．
（1）按照上述两个根式的化简过程的基本思想，将
10-2
21
化简；
（2）针对上述各式反映的规律，请你写出
a±2
b
=
m
±
n
(m＞0)中a，b与m，n之间的关系．
（附加题）观察下列各式：-1×
1
2
=-1+
1
2
；-
1
2
×
1
3
=-
1
2
+
1
3
；-
1
3
×
1
4
=-
1
3
+
1
4
；-
1
4
×
1
5
=-
1
4
+
1
5
…
（1）探索其运算规律，并用n（n为正整数）的代数式表示为
 
；
（2）试运用你发现的规律计算：(-1×
1
2
)+(-
1
2
×
1
3
)+(-
1
3
×
1
4
)+(-
1
4
×
1
5
)+…+(-
1
2010
×
1
2011
)
附加题：观察下列各式：
1×2=
1
3
(1×2×3-0×1×2)
2×3=
1
3
(2×3×4-1×2×3)
3×4=
1
3
(3×4×5-2×3×4)
…
计算：3×（1×2+2×3+3×4+…+99×100）=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网