题目内容
附加题阅读、理解和探索(1)观察下列各式:①
| 1 |
| 1×2 |
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
(2)利用(1)中的规律,计算:
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 9×10 |
(3)应用以上规律化简:
| 1 |
| n(n+1) |
| 1 |
| (n+1)(n+2) |
| 1 |
| (n+2)(n+3) |
| 1 |
| (n+2008)(n+2009) |
(4)观察按规律排列一组数:
| 1 |
| 3 |
| 1 |
| 15 |
| 1 |
| 35 |
| 1 |
| 3 |
| 1 |
| 15 |
| 1 |
| 35 |
分析:根据题中所给的式子分析可得出结果.注意分母之间的关系.即
=
-
| 1 |
| n×(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
解答:解:根据以上分析故(1)第④个式子是
=
-
,第n个式子是
=
-
.
(2)解:
+
+
+…+
=1-
+
-
+
-
+…+
-
=1-
=
(3)解:原式=
-
+
-
+…+
-
=
-
=
(4)把第n项填入括号:
+
+
+…+(
)可得原式=
(1-
)+
(
-
)+
(
-
)+
(
-
)
=
(1-
+
-
+
-
+…+
-
)
=
(1-
)=
×
=
| 1 |
| 4×5 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
(2)解:
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 9×10 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 9 |
| 1 |
| 10 |
| 1 |
| 10 |
| 9 |
| 10 |
(3)解:原式=
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| n+2008 |
| 1 |
| n+2009 |
| 1 |
| n |
| 1 |
| n+2009 |
| 2009 |
| n(n+2009) |
(4)把第n项填入括号:
| 1 |
| 3 |
| 1 |
| 15 |
| 1 |
| 35 |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
=
| 1 |
| 2 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
| 2n |
| 2n+1 |
| n |
| 2n+1 |
点评:主要考查了学生的分析、总结、归纳能力,规律型的习题一般是从所给的数据和运算方法进行分析,从特殊值的规律上总结出一般性的规律.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 附加题
附加题 表示5与2差的绝对值,也可理解为5与2两数在数轴上所
表示5与2差的绝对值,也可理解为5与2两数在数轴上所  可以看做
可以看做 ,表示5与-2的差的绝对值,也
,表示5与-2的差的绝对值,也 ,使
,使 是否有最小值? 如果有,写出最
是否有最小值? 如果有,写出最  表示5与2差的绝对值,也可理解为5与2两数在数轴上所
表示5与2差的绝对值,也可理解为5与2两数在数轴上所  可以看做
可以看做 ,表示5与-2的差的绝对值,也
,表示5与-2的差的绝对值,也 ,使
,使 是否有最小值? 如果有,写出最
是否有最小值? 如果有,写出最  ;②
;② ;③
;③ ;…用你发现的规律写出:第④个式子是(______),第n个式子是(______);
;…用你发现的规律写出:第④个式子是(______),第n个式子是(______);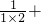
 +
+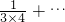 +
+ ;
;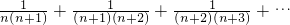 +
+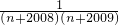 ;
;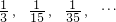 ,猜想第n个数是什么(请用含n的式子表达)把它填入求这组数的前n项和:
,猜想第n个数是什么(请用含n的式子表达)把它填入求这组数的前n项和: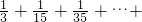 (______)中的括号内,并把这个和式化简.
(______)中的括号内,并把这个和式化简.