ΧβΡΩΡΎ»ί
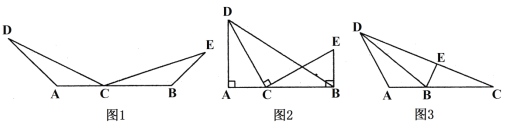
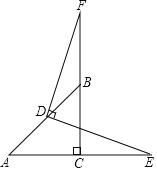
ΓΨΧβΡΩΓΩ»γΆΦ 1Θ§‘ΎΨΊ–Έ ABCD ÷–Θ§ABΘΫ8Θ§ADΘΫ10Θ§E « CD ±Ώ…œ“ΜΒψΘ§Ν§Ϋ” AEΘ§ΫΪΨΊ–Έ ABCD ―Ί AE ’έΒΰΘ§ΕΞΒψ D «ΓΚΟ¬δ‘Ύ BC ±Ώ…œΒψ F ¥ΠΘ§―”≥Λ AE ΫΜ BC ΒΡ―”≥ΛœΏ”ΎΒψGΘ°
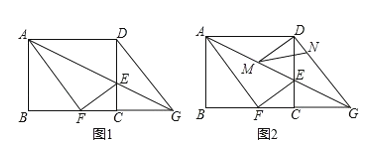
Θ®1Θ©«σœΏΕΈ CE ΒΡ≥ΛΘΜ
Θ®2Θ©»γΆΦ 2Θ§MΘ§N Ζ÷±π «œΏΕΈ AGΘ§DG …œΒΡΕ·ΒψΘ®”κΕΥΒψ≤Μ÷ΊΚœΘ©Θ§«“ΓœDMNΘΫΓœDAMΘ§ …η DNΘΫxΘ°
ΔΌ«σ÷ΛΥΡ±Ώ–Έ AFGD ΈΣΝβ–ΈΘΜ
ΔΎ «Ζώ¥φ‘Ύ’β―υΒΡΒψ NΘ§ ΙΓςDMN «÷±Ϋ«»ΐΫ«–ΈΘΩ»τ¥φ‘ΎΘ§«κ«σ≥ω x ΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§ «κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©CE=3ΘΜΘ®2Θ©ΔΌΦϊΫβΈωΘΜΔΎ![]() Μρ2Θ°
Μρ2Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©”…Ζ≠’έΩ…÷ΣΘΚADΘΫAFΘΫ10Θ°DEΘΫEFΘ§…ηECΘΫxΘ§‘ρDEΘΫEFΘΫ8xΘ°‘ΎRtΓςECF÷–Θ§άϊ”ΟΙ¥Ι…Ε®άμΙΙΫ®ΖΫ≥ΧΦ¥Ω…ΫβΨωΈ ΧβΘ°
Θ®2Θ©ΔΌ”…ΓςADEΓΉΓςGCEΦΤΥψ≥ωGCΒΡ≥ΛΕ»Θ§‘Ό÷ΛΟςΥΡ±Ώ–ΈAFGD «ΤΫ––ΥΡ±Ώ–ΈΘ§ΗυΨί“ΜΉιΝΎ±ΏœύΒ»ΒΡΤΫ––ΥΡ±Ώ–ΈΒΡΝβ–ΈΦ¥Ω…÷ΛΟςΘΜ
ΔΎ»τΓςDMN «÷±Ϋ«»ΐΫ«–ΈΘ§‘ρ”–ΝΫ÷÷«ιΩωΘ§“Μ «Β±ΓœMDN=90Γψ ±Θ§Εΰ «Β±ΓœDNM=90Γψ ±Θ§Ζ÷±πάϊ”ΟœύΥΤ»ΐΫ«–ΈΒΡ–‘÷ “‘ΦΑ»ώΫ«»ΐΫ«Κ· ΐΒΡΕ®“εΦ¥Ω…ΦΤΥψΒΟ≥ωΘ°
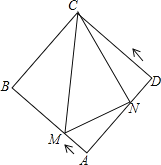
ΫβΘΚΘ®1Θ©ΓΏΥΡ±Ώ–ΈABCD «ΨΊ–ΈΘ§
ΓύADΘΫBCΘΫ10Θ§ABΘΫCDΘΫ8Θ§
ΓύΓœBΘΫΓœBCDΘΫ90ΓψΘ§
”…Ζ≠’έΩ…÷ΣΘΚADΘΫAFΘΫ10Θ°DEΘΫEFΘ§…ηCEΘΫxΘ§‘ρDEΘΫEFΘΫ8xΘ°
‘ΎRtΓςABF÷–Θ§BFΘΫ![]() Θ§
Θ§
ΓύCFΘΫBCBFΘΫ106ΘΫ4Θ§
‘ΎRtΓςEFC÷–Θ§‘ρ”–ΘΚ(8x)2ΘΫx2ΘΪ42Θ§
ΓύxΘΫ3Θ§
ΓύCEΘΫ3Θ°
Θ®2Θ©ΔΌ÷ΛΟςΘΚΓΏΥΡ±Ώ–ΈABCD «ΨΊ–ΈΘ§
ΓύADΓΈBC
ΓύΓςADEΓΉΓςGCEΘ§
Γύ![]() Θ§
Θ§
ΓΏAD=10Θ§CE=3Θ§DE=5Θ§
Γύ![]() Θ§
Θ§
ΓύGC=6Θ§
”…Θ®1Θ©Ω…ΒΟΘΚCF=4Θ§
ΓύGF=6+4=10Θ§
ΓύΥΡ±Ώ–ΈAFGD «ΤΫ––ΥΡ±Ώ–ΈΘ§
”÷ΓΏAD=AFΘ§
ΓύΤΫ––ΥΡ±Ώ–ΈAFGD «Νβ–ΈΘ°
ΔΎΓΏΓœDMN=ΓœDAMΘ§
Γύ»τΓςDMN «÷±Ϋ«»ΐΫ«–ΈΘ§‘ρ”–ΝΫ÷÷«ιΩωΘ§
Β±ΓœMDN=90Γψ ±Θ§
ÿAD=GDȧ
ΓύΓœDAG=ΓœDGA
”÷ΓΏΓœADE=ΓœGDM=90ΓψΘ§
ΓύΓςADEΓ’ΓςGDMΘ®ASAΘ©
ΓύDM=DE=5Θ§
”÷ΓΏΓœDMN=ΓœDAMΘ§ΓœADE=ΓœMDN=90ΓψΘ§
ΓύΓςADEΓΉΓςMDN
Γύ![]() Θ§Φ¥
Θ§Φ¥![]() Θ§
Θ§
Γύ![]() ΘΜ
ΘΜ
Β±ΓœDNM=90Γψ ±Θ§‘ρΓœMDN+ΓœDMN=90ΓψΘ§
”÷ΓΏΓœDMN=ΓœDAMΘ§ΓœDAG=ΓœDGAΘ§
ΓύΓœDMN=ΓœDGAΘ§
ΓύΓœMDN+ΓœDGA=90ΓψΘ§
ΓύΓœDMG=90ΓψΘ§
ΓΏsinΓœDAE=![]() Θ§
Θ§
ΓΏ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
ΓύDM=![]() Θ§
Θ§
ΓΏΓœDMN=ΓœDAM
ΓύsinΓœDMN=sinΓœDAM
Γύ![]() Θ§Φ¥
Θ§Φ¥![]()
ΫβΒΟΘΚx=2Θ§
Ήέ…œΥυ ωΘΚ![]() Μρ2Θ°
Μρ2Θ°

 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ