题目内容
【题目】在△ABC中,∠ACB=90°,AC=BC,D为AB的中点,点E为AC延长线上一点,连接DE,过点D作DF⊥DE交CB的延长线于点F.
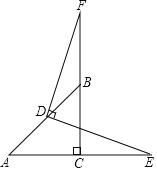
(1)求证:BF=CE;
(2)若CE=AC,用等式表示线段DF与AB的数量关系,并证明.
【答案】(1)详见解析;(2)DF![]() AB.
AB.
【解析】
(1)连接DC,由等腰直角△ABC的中线得CD=BD;等腰直角△ABC顶角平分线和底角,∠ABC与∠ABF互为邻补角,由∠BCE=90°,∠DCB=45°,计算出∠DBF=∠DCB=135°;∠CHE+∠E=90°;∠CHE=∠DHF等量代换得∠F=∠E,从而证明△DBF≌△DCE,最后根据全等三角形的性质求BF=CE.
(2)连接BE,在△DCE中,点D和C分别是AB和AE的中点,得到DC∥BE,在(1)基础上易证∠ABE=90°,AB=BE.计算出线段DE的长度与线段AB的关系,即求出线段DF与线段AB的关系.
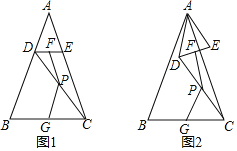
(1)连接CD,DE与CF相交于点H,如图1所示:

∵在Rt△ABC中,D为AB中点,
∴CD=BD,
又∵AC=BC,
∴DC⊥AB,
∴∠ABC=∠DCB=45°,
∵∠ACB=90°,
∴∠BCE=90°,
∵∠ABC+∠ABF=180°,∠DCE=∠DCB+∠BCE,
∴∠DBF=180°﹣45°=135°,∠DCB=90°+45°=135°,
∴∠DBF=∠DCB,
∵DF⊥DE,
∴∠DHF+∠F=90°,
又∵∠CHE+∠E=90°;∠CHE=∠DHF,
∴∠F=∠E,
在△DBF和△DCE中
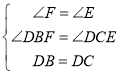 ,
,
∴△DBF≌△DCE(AAS),
∴BF=CE.
(2)线段DF与AB的数量关系:DF![]() AB.
AB.
连接BE,设AD=BD=a,则AB=2a.如图2所示

∵△DBF≌△DCE,
∴DF=DE.
∵CE=AC,DA=DB,
∴DC∥BE,
又∵∠ADC=90°,
∴∠ABE=90°,
∵∠A=45°,
∴∠AEB=45°,
∴AB=BE=2a,
在Rt△BDE中,由勾股定理得:
DE2=DB2+BE2,
∴DE![]() ,
,
∴DF![]() a,
a,
∴![]() .
.
即DF![]() AB.
AB.

 阅读快车系列答案
阅读快车系列答案