题目内容
已知:如图,∠MAN=45°,B为AM上的一个定点.若点P在射线AN上,以P为圆心,PA为半径的圆与射线AN的另一个交点为C.请确定⊙P的位置,使BC恰与⊙P相切.
(1)画出⊙P;(不要求尺规作图,不要求写画法)
(2)连接BC、BP并填空:
①∠ABC=______°;
②比较大小:∠ABP______∠CBP.(用“>”“<”或“=”连接))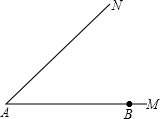
(1)画出⊙P;(不要求尺规作图,不要求写画法)
(2)连接BC、BP并填空:
①∠ABC=______°;
②比较大小:∠ABP______∠CBP.(用“>”“<”或“=”连接))

(1)图形见右. (2分)
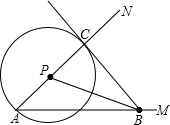
(2)①∵⊙P与BC相切,C为切点,
∴BC⊥AC,∠ACB=90°.
∵∠MAN=45°,∴∠ABC=45°;(3分)
②∠ABP<∠CBP. (4分)
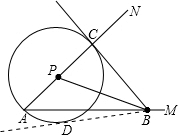
理由:过B点作⊙P的另一条切线BD,切点为D.
则∠CBP=∠DBP.
又∠DBP>∠ABP,
∴∠ABP<∠CBP.


(2)①∵⊙P与BC相切,C为切点,
∴BC⊥AC,∠ACB=90°.
∵∠MAN=45°,∴∠ABC=45°;(3分)
②∠ABP<∠CBP. (4分)
理由:过B点作⊙P的另一条切线BD,切点为D.
则∠CBP=∠DBP.
又∠DBP>∠ABP,
∴∠ABP<∠CBP.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 18、已知:如图,∠MAN=45°,B为AM上的一个定点.若点P在射线AN上,以P为圆心,PA为半径的圆与射线AN的另一个交点为C.请确定⊙P的位置,使BC恰与⊙P相切.
18、已知:如图,∠MAN=45°,B为AM上的一个定点.若点P在射线AN上,以P为圆心,PA为半径的圆与射线AN的另一个交点为C.请确定⊙P的位置,使BC恰与⊙P相切. 已知:如图,∠MAN=30°,O为边AN上一点,以O为圆心,2为半径作⊙O,交AN于D,E两点,当AD=
已知:如图,∠MAN=30°,O为边AN上一点,以O为圆心,2为半径作⊙O,交AN于D,E两点,当AD= 22、已知:如图,∠MAN=30°,点O为AN上一点,以O为圆心,2为半径作⊙O,交AN于D、E两点,⊙O与AM相切时,求AD的长.
22、已知:如图,∠MAN=30°,点O为AN上一点,以O为圆心,2为半径作⊙O,交AN于D、E两点,⊙O与AM相切时,求AD的长.
