��Ŀ����
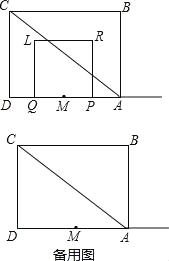
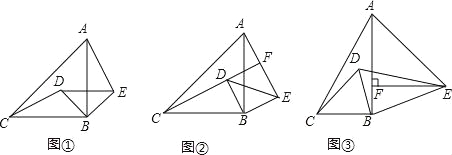
����Ŀ���Ķ����֣���1����ͼ�٣���Rt��ABC��Rt��DBE�У���ABC=��DBE=90�㣬AB=BC=3��BD=BE=1������CD��AE����֤����BCD�ա�BAE��������Ҫ֤����
������⣺��2���ڣ�1���������£���BD��AEʱ���ӳ�CD��AE�ڵ�F����ͼ�ڣ���AF�ij���
������⣺��3����ͼ�ۣ���Rt��ABC��Rt��DBE�У���ABC=��DBE=90�㣬��BAC=��DEB=30�㣬����CD��AE������BAE=45��ʱ����E��AB�ľ���EF�ij�Ϊ2�����߶�CD�ij�Ϊ ��
���𰸡���2��AF=2![]() ��1��
��1��
��3��![]() ��
��
��������
�����������2������BCD�ա�BAE���õ���OAF=��OCB�����ݡ�8���͡�֤����AFO=��CBO=90�㣬��RT��BDC�����ù��ɶ������CD����֤��BD=EF���ɽ�����⣮
��3���������߳ɱ����н���������������ƣ�����֤����ABE�ס�CBD����![]() �������AE���ɽ�����⣮
�������AE���ɽ�����⣮
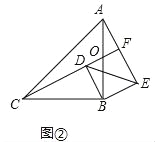
�����������2����ͼ���У�AB��CF���ڵ�O��
�ɣ�1����֪����BCD�ա�BAE��
���OAF=��OCB��CD=AE���ߡ�AOF=��COB��
���AFO=��CBO=90�㣬
��CF��AE����BD��AE��
��BD��CF��
��RT��CDB�У��ߡ�CDB=90�㣬BC=3��BD=1��
��CD=AE=![]() =2
=2![]() ��
��
�ߡ�BDF=��DFE=��DBE=90�㣬
���ı���EFDB�Ǿ��Σ�
��EF=BD=1��
��AF=AE��EF=2![]() ��1��
��1��
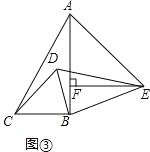
��3����RT��ABC��RT��EBD�У��ߡ�ABC=��DBE=90�㣬��BAC=��DEB=30�㣬
��AB=![]() BC��BE=
BC��BE=![]() BD��
BD��
��![]() ��
��
�ߡ�ABC=��EBD=90�㣬
���ABE=��DBC��
���ABE�ס�CBD��
��![]() ��
��
��RT��AEF�У��ߡ�AFE=90�㣬��EAF=45�㣬EF=2��
��AF=EF=2��AE=2![]() ��
��
��![]() ��
��
��CD=![]() ��
��
�ʴ�Ϊ![]() ��
��

 ȫ�ܲ��һ���þ�ϵ�д�
ȫ�ܲ��һ���þ�ϵ�д�