题目内容
【题目】如图,正方形ABCD,点E在CD上,连接AE,BD,点G是AE中点,过点G作FH⊥AE,FH分别交AD,BC于点F,H,FH与BD交于点K,且HK=2FG,若EG=![]() ,则线段AF的长为_______________.
,则线段AF的长为_______________.

【答案】![]()
【解析】
本题的解题关键是根据圆周角定理得出GK=EG,得到这个条件以后,再通过作辅助线,得到△MFH≌△ADE,得出FH的长,然后再根据已知计算即可.
如图,过H点向AD边做垂线,交AD于点M,
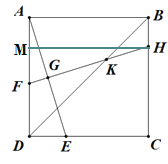
由题可知HM=AD,∠FMH=∠ADE=90°,
∵FH⊥AE,
∴∠FAG+∠AFG=90°,
∵∠ADE=90°,
∴∠FAG+∠AED=90°,
∴∠AED=∠AFG
∴△MFH≌△ADE,
∴FH=AE,
∵点G是AE中点,EG=![]() ,
,
∴FH=AE=![]()
由已知可得∠KDE=45°=![]() ∠HEG,
∠HEG,
∴点K位于以G点为圆心,以AE为直径的圆上,
∴AG=GK=EG=![]() ,
,
∴FG+HK=![]()
∵HK=2FG,
∴FG=![]() ,
,
根据勾股定理可得AF=![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目