题目内容
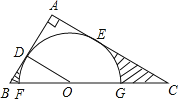
【题目】已知:如图,五边形ABCDE中,AE∥BC,∠A+∠B=α,∠C+∠D+∠E=β,猜想α与β的数量关系并写出你的证明.
(1)根据图形写出你的猜想: ;
(2)请证明你在(1)中写出的猜想.

【答案】(1)β=2α;(2)证明见解析.
【解析】试题分析:(1)可猜想为β=2α;
(2)过D作DF∥AE,根据平行线的性质由AE∥BC得到∠A+∠B=α=180°,∠EDF+∠E=180°,由于AE∥BC,则DF∥BC,所以∠CDF+∠C=180°,则∠E+∠EDC+∠C=β=360°,于是有β=2α.
试题解析:(1)β=2α;
(2)证明:过D作DF∥AE,
∵AE∥BC,
∴∠A+∠B=α=180°,
∵DF∥AE,
∴∠EDF+∠E=180°,
∵AE∥BC,
∴DF∥BC,
∴∠CDF+∠C=180°,
∴∠E+∠EDC+∠C=360°,
∵∠E+∠EDC+∠C=β,
∴β=360°.
∴β=2α.


练习册系列答案
相关题目