题目内容
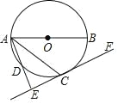
【题目】如图,AB为⊙O的直径,点C,D在⊙O上,且点C是![]() 的中点,过点 C作AD的垂线 EF交直线 AD于点 E.
的中点,过点 C作AD的垂线 EF交直线 AD于点 E.
(1)求证:EF是⊙O的切线;
(2)连接BC,若AB=5,BC=3,求线段AE的长.
【答案】(1)证明见解析
(2)![]()
【解析】
(1)连接OC,根据等腰三角形的性质、平行线的判定得到OC∥AE,得到OC⊥EF,根据切线的判定定理证明;
(2)根据勾股定理求出AC,证明△AEC∽△ACB,根据相似三角形的性质列出比例式,计算即可.
(1)证明:连接OC,
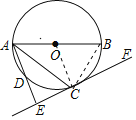
∵OA=OC,
∴∠OCA=∠BAC,
∵点C是![]() 的中点,
的中点,
∴∠EAC=∠BAC,
∴∠EAC=∠OCA,
∴OC∥AE,
∵AE⊥EF,
∴OC⊥EF,即EF是⊙O的切线;
(2)解:∵AB为⊙O的直径,
∴∠BCA=90°,
∴AC=![]() =4,
=4,
∵∠EAC=∠BAC,∠AEC=∠ACB=90°,
∴△AEC∽△ACB,
∴![]() ,
,
∴AE=![]() .
.

练习册系列答案
相关题目
【题目】小华有一个容最为8![]() (
(![]() )的
)的![]() 盘,
盘,![]() 盘中已经存储了一个视频文件,其余空间都用来存储照片,且每张照片占用的内存容量均相同,已知剩余可用空间
盘中已经存储了一个视频文件,其余空间都用来存储照片,且每张照片占用的内存容量均相同,已知剩余可用空间![]() 与图片数量
与图片数量![]() (张)满足一次函数关系,对应数据如下表:
(张)满足一次函数关系,对应数据如下表:
图片数量 | 100 | 150 |
剩余可用空间 | 5700 | 5550 |
(1)求出![]() 与
与![]() 之间的关系式,并求出
之间的关系式,并求出![]() 盘中视频文件占用的内存容量;
盘中视频文件占用的内存容量;
(2)若![]() 盘中已经存入1280张照片,那么最多还能存入多少张照片?
盘中已经存入1280张照片,那么最多还能存入多少张照片?