题目内容
【题目】如图,过∠AOB的平分线上一点C作CD∥OB交OA于点D,E是线段OC的中点,过点E作直线分别交射线CD,OB于点M,N,探究线段OD,ON,DM之间的数量关系,并证明你的结论.

【答案】OD=DM+ON
【解析】试题分析:分两种情况讨论,①当M在线段CD上时,由OC是∠AOB的平分线,CD∥OB,得出∠DOC=∠DC0,故有OD=CD=DM+CM;再由E是线段OC的中点,CD∥OB,得到CM=ON,即可得出OD=DM+ON;
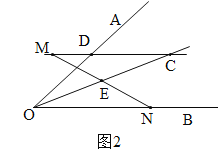
②当M在线段CD延长线上时,OD=ON-DM,如图2,同①可得OD=DC=CM-DM=ON-DM.
试题解析:①当M在线段CD上时,OD=DM+ON.证明如下:
∵OC是∠AOB的平分线,∴∠DOC=∠C0B,又∵CD∥OB,∴∠DCO=∠C0B,∴∠DOC=∠DC0,∴OD=CD=DM+CM,∵E是线段OC的中点,∴CE=OE,∵CD∥OB,∴![]() ,∴CM=ON,又∵OD=DM+CM,∴OD=DM+ON;
,∴CM=ON,又∵OD=DM+CM,∴OD=DM+ON;
②当M在线段CD延长线上时,OD=ON-DM,如图2,同①可得OD=DC=CM-DM=ON-DM.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目



