��Ŀ����
��֪��ͼ��������y=ax2+bx-a��ͼ����x�ύ��A��B���㣬��A�ڵ�B����ߣ���������ΪC��0��-4����ֱ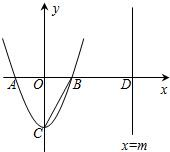 ��x=m��m��1����x�ύ�ڵ�D��
��x=m��m��1����x�ύ�ڵ�D����1���������ߵĽ���ʽ��
��2����ֱ��x=m��m��1������һ��P����P�ڵ�һ���ޣ���ʹ����P��D��BΪ���������������B��C��OΪ��������������ƣ���P�����꣨�ú�m�Ĵ���ʽ��ʾ����
��3���ڣ�2�������������£����ʣ�������y=ax2+bx-a�Ƿ����һ��Q��ʹ���ı���ABPQΪƽ���ı��Σ�������������ĵ�Q�������m��ֵ����������ڣ����Ҫ˵�����ɣ�
��������1�����������ߵĶ���������y���ϣ�������Ϊ��0��-4�����������ߵĶԳ���Ϊy�ᣬ��b=0��a=4���ɴ�ȷ���������ߵĽ���ʽ��
��2�������P�������꣬���������ߵĽ���ʽ�������B������꣬�����ɵ�OC=4OB����BOC�͡�ODB�У�����m��ʾ��BD�ij���������ֱ�����������ƣ���ôֱ�DZ߶�Ӧ�ɱ�������PD=4BD��BD=4PD���ɴ���õ�P�������꣬�����ɵõ���P�����꣮
��3�����ı���ABPQΪƽ���ı��Σ���ôPQ=AB=2����ô����P����������ƽ��2����λ���ɵõ���Q�����꣬Ȼ��Q��������������ߵĽ���ʽ�м������m��ֵ��
��2�������P�������꣬���������ߵĽ���ʽ�������B������꣬�����ɵ�OC=4OB����BOC�͡�ODB�У�����m��ʾ��BD�ij���������ֱ�����������ƣ���ôֱ�DZ߶�Ӧ�ɱ�������PD=4BD��BD=4PD���ɴ���õ�P�������꣬�����ɵõ���P�����꣮
��3�����ı���ABPQΪƽ���ı��Σ���ôPQ=AB=2����ô����P����������ƽ��2����λ���ɵõ���Q�����꣬Ȼ��Q��������������ߵĽ���ʽ�м������m��ֵ��
���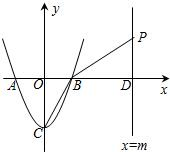 �⣺��1����������y=ax2+bx-a�Ķ�������ΪC��0��-4����
�⣺��1����������y=ax2+bx-a�Ķ�������ΪC��0��-4����
��b=0��a=4��
�������ߵĽ���ʽΪy=4x2-4����2�֣�
��2����P��m��n������4x2-4=0��
��x=��1��
��A��-1��0����B��1��0����
�ߡ�OBC�ס�PBD��
����OCB=��PBD����
=
��
��
=
��
��n=
(m-1)��
��ʱP(m��
)����4�֣�
����OCB=��BPD����
=
��
��
=
��
��n=4��m-1����
��ʱP��m��4��m-1��������6�֣�
��3�����������ߴ��ڵ�Q��x��y��ʹ�ı���ABPQΪƽ���ı��Σ�
��P��m��4m-4��ʱ��AP���е�R������Ϊ��R(
��2(m-1))��
�֡�R����BQ���е㣬
��
��Q��m-2��4��m-1������
��Q���������ϣ�
��4��m-1��=4��m-2��2-4��
��m-1=m2-4m+4-1��
��m2-5m+4=0��
��m=4��m=1����ȥ������8�֣�
��P������Ϊ(m��
)ʱ��
ͬ����R(
��
)��Q(m-2��
)��
�ߵ�Q���������ϣ�
��
=4•(m-2)2-4��
��16m2-65m+49=0��m=
��m=1����ȥ������10�֣�
�൱m=4��
ʱ��AP��BQ����ƽ�֣��ı���ABPQ��ƽ���ı��Σ�
��m=4��
Ϊ����11�֣�
��3�����⣺����AB=PQ=2��
��Q(m-2��
)��Q��m-2��4��m-1������
�ߵ�Q���������ϣ�
��4��m-2��2-4=4��m-1����
��֮m=
��m=1����m=4��m=1��
��m��1��
��m=4��
��
 �⣺��1����������y=ax2+bx-a�Ķ�������ΪC��0��-4����
�⣺��1����������y=ax2+bx-a�Ķ�������ΪC��0��-4������b=0��a=4��
�������ߵĽ���ʽΪy=4x2-4����2�֣�
��2����P��m��n������4x2-4=0��
��x=��1��
��A��-1��0����B��1��0����
�ߡ�OBC�ס�PBD��
����OCB=��PBD����
| OB |
| PD |
| OC |
| BD |
��
| 1 |
| n |
| 4 |
| m-1 |
��n=
| 1 |
| 4 |
��ʱP(m��
| m-1 |
| 4 |
����OCB=��BPD����
| OB |
| BD |
| OC |
| PD |
��
| 1 |
| m-1 |
| 4 |
| n |
��n=4��m-1����
��ʱP��m��4��m-1��������6�֣�
��3�����������ߴ��ڵ�Q��x��y��ʹ�ı���ABPQΪƽ���ı��Σ�
��P��m��4m-4��ʱ��AP���е�R������Ϊ��R(
| m-1 |
| 2 |
�֡�R����BQ���е㣬
��
|
��Q���������ϣ�
��4��m-1��=4��m-2��2-4��
��m-1=m2-4m+4-1��
��m2-5m+4=0��
��m=4��m=1����ȥ������8�֣�
��P������Ϊ(m��
| m-1 |
| 4 |
ͬ����R(
| m-1 |
| 2 |
| m-1 |
| 8 |
| m-1 |
| 4 |
�ߵ�Q���������ϣ�
��
| m-1 |
| 4 |
��16m2-65m+49=0��m=
| 49 |
| 16 |
�൱m=4��
| 49 |
| 16 |
��m=4��
| 49 |
| 16 |
��3�����⣺����AB=PQ=2��
��Q(m-2��
| m-1 |
| 4 |
�ߵ�Q���������ϣ�
��4��m-2��2-4=4��m-1����
��֮m=
| 49 |
| 16 |
��m��1��
��m=4��
| 49 |
| 16 |
������������Ҫ�����˶��κ�������ʽ��ȷ�������������ε��ж������ʡ�ƽ���ı��ε��ж������ʵ�֪ʶ�������������εĶ�Ӧ�ǺͶ�Ӧ�߲�ȷ��������£�һ��Ҫע��������ۣ�����©�⣮

��ϰ��ϵ�д�
�����Ŀ
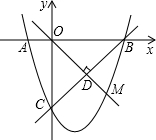 ��֪��ͼ��������y=ax2+bx+c����A��-1��0�����Ҿ���ֱ��y=x-3�����������������B��C��
��֪��ͼ��������y=ax2+bx+c����A��-1��0�����Ҿ���ֱ��y=x-3�����������������B��C�� ��֪��ͼ��������y=x2-x-1��y�ύ��C�㣬��ԭ��OΪԲ�ģ���OCΪ�뾶����O����x����A��B���㣬��y������һ��D�����PΪ������y=x2-x-1�ϵ�һ�㣬��PM��x���ڵ�M����ʹ��PMB�ס�ADBʱ��P�����꣮
��֪��ͼ��������y=x2-x-1��y�ύ��C�㣬��ԭ��OΪԲ�ģ���OCΪ�뾶����O����x����A��B���㣬��y������һ��D�����PΪ������y=x2-x-1�ϵ�һ�㣬��PM��x���ڵ�M����ʹ��PMB�ס�ADBʱ��P�����꣮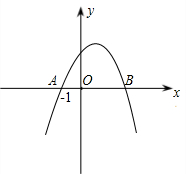 ��֪��ͼ��������y=ax2+bx+c��x�ύ�ڵ�A��-1��0���͵�B������
��֪��ͼ��������y=ax2+bx+c��x�ύ�ڵ�A��-1��0���͵�B������ ��֪��ͼ��������y=ax2+bx+c��x���ཻ��B��1��0����C��4��0�����㣬��y����������ཻ��A�㣬��A��B��C����ġ�P��y�������ڵ�A��
��֪��ͼ��������y=ax2+bx+c��x���ཻ��B��1��0����C��4��0�����㣬��y����������ཻ��A�㣬��A��B��C����ġ�P��y�������ڵ�A��