题目内容
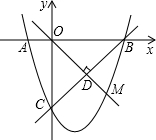 已知如图,抛物线y=ax2+bx+c过点A(-1,0),且经过直线y=x-3与坐标轴的两个交点B、C.
已知如图,抛物线y=ax2+bx+c过点A(-1,0),且经过直线y=x-3与坐标轴的两个交点B、C.(1)求抛物线的解析式;
(2)求抛物线的顶点坐标;
(3)若点M在第四象限内的抛物线上,且OM⊥BC,垂足为D,求点M的坐标.
分析:(1)先根据直线y=x-3求出B、C的坐标,然后将A、B、C的坐标代入抛物线中即可求得抛物线的解析式.
(2)根据(1)的抛物线的解析式用配方或公式法均可求出顶点坐标.
(3)已知了直线BC的解析式,由于OD⊥BC,因此直线OD的斜率与直线BC的斜率的乘积为-1,据此可求出直线OD的解析式.联立直线OD的解析式和抛物线的解析式即可求出M点的坐标.
(2)根据(1)的抛物线的解析式用配方或公式法均可求出顶点坐标.
(3)已知了直线BC的解析式,由于OD⊥BC,因此直线OD的斜率与直线BC的斜率的乘积为-1,据此可求出直线OD的解析式.联立直线OD的解析式和抛物线的解析式即可求出M点的坐标.
解答:解:(1)易知:B(3,0),C(0,-3),
设抛物线的解析式为y=a(x+1)(x-3),则有:
a(0+1)(0-3)=-3,a=1,
∴y=x2-2x-3.
(2)由(1)知:y=x2-2x-3=(x-1)2-4,
因此顶点坐标为(1,-4).
(3)由于直线OD⊥BC,
因此直线OD的解析式为y=-x,
联立抛物线则有:
,
解得
,
,
由于点M在第四象限,因此M(
,
).
设抛物线的解析式为y=a(x+1)(x-3),则有:
a(0+1)(0-3)=-3,a=1,
∴y=x2-2x-3.
(2)由(1)知:y=x2-2x-3=(x-1)2-4,
因此顶点坐标为(1,-4).
(3)由于直线OD⊥BC,
因此直线OD的解析式为y=-x,
联立抛物线则有:
|
解得
|
|
由于点M在第四象限,因此M(
1+
| ||
| 2 |
-1-
| ||
| 2 |
点评:本题考查了二次函数解析式的确定、函数图象的交点等知识点.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
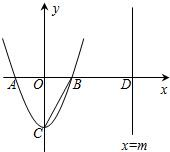 线x=m(m>1)与x轴交于点D.
线x=m(m>1)与x轴交于点D. 已知如图,抛物线y=x2-x-1与y轴交于C点,以原点O为圆心,以OC为半径作⊙O,交x轴于A、B两点,交y轴于另一点D.设点P为抛物线y=x2-x-1上的一点,作PM⊥x轴于点M,求使△PMB∽△ADB时的P点坐标.
已知如图,抛物线y=x2-x-1与y轴交于C点,以原点O为圆心,以OC为半径作⊙O,交x轴于A、B两点,交y轴于另一点D.设点P为抛物线y=x2-x-1上的一点,作PM⊥x轴于点M,求使△PMB∽△ADB时的P点坐标.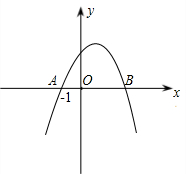 已知如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0)和点B,化简
已知如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0)和点B,化简 已知如图,抛物线y=ax2+bx+c与x轴相交于B(1,0)、C(4,0)两点,与y轴的正半轴相交于A点,过A、B、C三点的⊙P与y轴相切于点A.
已知如图,抛物线y=ax2+bx+c与x轴相交于B(1,0)、C(4,0)两点,与y轴的正半轴相交于A点,过A、B、C三点的⊙P与y轴相切于点A.