题目内容
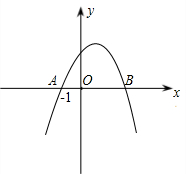 已知如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0)和点B,化简
已知如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0)和点B,化简| (a+c)2 |
| (c-b)2 |
| A、一个 | B、两个 | C、三个 | D、四个 |
分析:先把A点坐标代入抛物线的解析式可得a-b+c=0,再根据抛物线的开口向下可得a<0,由抛物线的图象可知对称轴在x轴的正半轴可知-
>0,抛物线与y轴相交于y轴的正半轴,所以c>0,根据此条件即可判断出a+c及c-b的符号,再根据二次根式的性质即可进行解答.
| b |
| 2a |
解答:解:∵抛物线y=ax2+bx+c与x轴交于点A(-1,0),
∴a-b+c=0,即a+c=b,
∵抛物线的开口向下,
∴a<0,
∵对称轴在x轴的正半轴可知-
>0,
∴b>0,
∵抛物线与y轴相交于y轴的正半轴,
∴c>0,
∴a+c=b>0,c>b,
∴①原式=b+(c-b)=c,故①正确,
④原式=a+c+c-b=a-b+2c,故④正确.
③∵a-b+c=0
∴原式=a-b+2c=a-b+c+c=0+c=c,故③正确.
故选C.
∴a-b+c=0,即a+c=b,
∵抛物线的开口向下,
∴a<0,
∵对称轴在x轴的正半轴可知-
| b |
| 2a |
∴b>0,
∵抛物线与y轴相交于y轴的正半轴,
∴c>0,
∴a+c=b>0,c>b,
∴①原式=b+(c-b)=c,故①正确,
④原式=a+c+c-b=a-b+2c,故④正确.
③∵a-b+c=0
∴原式=a-b+2c=a-b+c+c=0+c=c,故③正确.
故选C.
点评:本题考查的是抛物线与x轴的交点,涉及到抛物线的图象与系数的关系,抛物线的对称轴方程等相关知识.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 已知如图,抛物线y=ax2+bx+c过点A(-1,0),且经过直线y=x-3与坐标轴的两个交点B、C.
已知如图,抛物线y=ax2+bx+c过点A(-1,0),且经过直线y=x-3与坐标轴的两个交点B、C.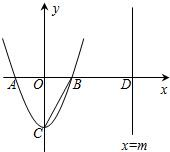 线x=m(m>1)与x轴交于点D.
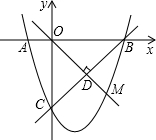
线x=m(m>1)与x轴交于点D. 已知如图,抛物线y=x2-x-1与y轴交于C点,以原点O为圆心,以OC为半径作⊙O,交x轴于A、B两点,交y轴于另一点D.设点P为抛物线y=x2-x-1上的一点,作PM⊥x轴于点M,求使△PMB∽△ADB时的P点坐标.
已知如图,抛物线y=x2-x-1与y轴交于C点,以原点O为圆心,以OC为半径作⊙O,交x轴于A、B两点,交y轴于另一点D.设点P为抛物线y=x2-x-1上的一点,作PM⊥x轴于点M,求使△PMB∽△ADB时的P点坐标. 已知如图,抛物线y=ax2+bx+c与x轴相交于B(1,0)、C(4,0)两点,与y轴的正半轴相交于A点,过A、B、C三点的⊙P与y轴相切于点A.
已知如图,抛物线y=ax2+bx+c与x轴相交于B(1,0)、C(4,0)两点,与y轴的正半轴相交于A点,过A、B、C三点的⊙P与y轴相切于点A.