题目内容
 已知如图,抛物线y=ax2+bx+c与x轴相交于B(1,0)、C(4,0)两点,与y轴的正半轴相交于A点,过A、B、C三点的⊙P与y轴相切于点A.
已知如图,抛物线y=ax2+bx+c与x轴相交于B(1,0)、C(4,0)两点,与y轴的正半轴相交于A点,过A、B、C三点的⊙P与y轴相切于点A.(1)请求出点A坐标和⊙P的半径;
(2)请确定抛物线的解析式;
(3)M为y轴负半轴上的一个动点,直线MB交⊙P于点D.若△AOB与以A、B、D为顶点的三角形相似,求MB•MD的值.(先画出符合题意的示意图再求解).
分析:(1)利用切割线定理以及矩形的性质得出点A坐标和⊙P的半径;
(2)将B(1,0)、C(4,0),A(0,2)带入y=ax2+bx+c求出a,b,c进而得出解析式即可;
(3)根据题意∠OAB=∠ADB,得出△AOB和△ABD相似有两种情况进而得出即可.
(2)将B(1,0)、C(4,0),A(0,2)带入y=ax2+bx+c求出a,b,c进而得出解析式即可;
(3)根据题意∠OAB=∠ADB,得出△AOB和△ABD相似有两种情况进而得出即可.
解答: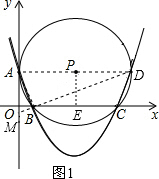 解:(1)∵OA是⊙P的切线,OC是⊙P的割线.
解:(1)∵OA是⊙P的切线,OC是⊙P的割线.
∴OA2=OB×OC,
即OA2=1×4,
∴OA=2,
即点A点坐标是(0,2)
如图1,连接PA,过P作PE⊥CO交OC于E显然,四边形PAOE为矩形,
故PA=OE,
∵PE⊥BC,
∴BE=CE,
又∵BC=3,
∴BE=
,
∴PA=OE=OB+BE=1+
=
,
即⊙P的半径长为
.
(2)将B(1,0)、C(4,0),A(0,2)带入y=ax2+bx+c得:
,
解得:
,
故抛物线的解析式是:y=
x2-
x+2;
(3)根据题意∠OAB=∠ADB,
所以△AOB和△ABD相似有两种情况
①∠ABD和∠AOB对应,
如图1,此时AD是⊙P的直径则AB=
,AD=5
∴BD=2
,
∵Rt△AMB∽Rt△DAB,
∴MA:AD=AB:BD,
即MA=
=
,
∵Rt△AMB∽Rt△DMA,
∴MA:MD=MB:MA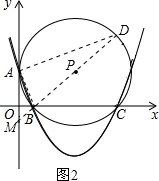
即MB•MD=MA2=
,
②∠BAD和∠AOB对应,
如图2,此时BD是⊙P的直径,所以直线MB过P点
∵B(1,0),P(
,2),
∴直线MB的解析式是:y=
x-
∴M点的坐标为(0,-
),
∴AM=
,
由△MAB∽△MDA,
得MA:MD=MB:MA
∴MB•MD=MA2=
.
 解:(1)∵OA是⊙P的切线,OC是⊙P的割线.
解:(1)∵OA是⊙P的切线,OC是⊙P的割线.∴OA2=OB×OC,
即OA2=1×4,
∴OA=2,
即点A点坐标是(0,2)
如图1,连接PA,过P作PE⊥CO交OC于E显然,四边形PAOE为矩形,
故PA=OE,
∵PE⊥BC,
∴BE=CE,
又∵BC=3,
∴BE=
| 3 |
| 2 |
∴PA=OE=OB+BE=1+
| 3 |
| 2 |
| 5 |
| 2 |
即⊙P的半径长为
| 5 |
| 2 |
(2)将B(1,0)、C(4,0),A(0,2)带入y=ax2+bx+c得:
|
解得:
|
故抛物线的解析式是:y=
| 1 |
| 2 |
| 5 |
| 2 |
(3)根据题意∠OAB=∠ADB,
所以△AOB和△ABD相似有两种情况
①∠ABD和∠AOB对应,
如图1,此时AD是⊙P的直径则AB=
| 5 |
∴BD=2
| 5 |
∵Rt△AMB∽Rt△DAB,
∴MA:AD=AB:BD,
即MA=
| AB•AD |
| BD |
| 5 |
| 2 |
∵Rt△AMB∽Rt△DMA,
∴MA:MD=MB:MA

即MB•MD=MA2=
| 25 |
| 4 |
②∠BAD和∠AOB对应,
如图2,此时BD是⊙P的直径,所以直线MB过P点
∵B(1,0),P(
| 5 |
| 2 |
∴直线MB的解析式是:y=
| 4 |
| 3 |
| 4 |
| 3 |
∴M点的坐标为(0,-
| 4 |
| 3 |
∴AM=
| 10 |
| 3 |
由△MAB∽△MDA,
得MA:MD=MB:MA
∴MB•MD=MA2=
| 100 |
| 9 |
点评:此题主要考查了二次函数的综合应用以及相似三角形的判定与性质等知识,根据已知得图形进行分类讨论是解题关键.

练习册系列答案
相关题目
 已知如图,抛物线y=ax2+bx+c过点A(-1,0),且经过直线y=x-3与坐标轴的两个交点B、C.
已知如图,抛物线y=ax2+bx+c过点A(-1,0),且经过直线y=x-3与坐标轴的两个交点B、C.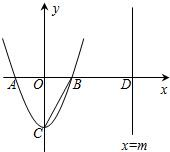 线x=m(m>1)与x轴交于点D.
线x=m(m>1)与x轴交于点D. 已知如图,抛物线y=x2-x-1与y轴交于C点,以原点O为圆心,以OC为半径作⊙O,交x轴于A、B两点,交y轴于另一点D.设点P为抛物线y=x2-x-1上的一点,作PM⊥x轴于点M,求使△PMB∽△ADB时的P点坐标.
已知如图,抛物线y=x2-x-1与y轴交于C点,以原点O为圆心,以OC为半径作⊙O,交x轴于A、B两点,交y轴于另一点D.设点P为抛物线y=x2-x-1上的一点,作PM⊥x轴于点M,求使△PMB∽△ADB时的P点坐标. 已知如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0)和点B,化简
已知如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0)和点B,化简