题目内容
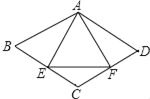
【题目】如图，菱形ABCD中，∠B=60°，AB=2，E，F分别是BC、CD的中点，连接AE、EF，则△AEF的周长为_____．
【答案】3
【解析】分析：根据菱形的性质和等边三角形的判定方法得，三角形ABC是等边三角形．则AE⊥BC，根据勾股定理求得AE的长，同理得到EF的长，根据已知可推出△AEF是等边三角形，从而得到其周长是3．
详解：连接AC，
∵四边形ABCD是菱形，
∴AB=BC，
∵∠B=60°，
∴△ABC为等边三角形，
∴AC=AB=AD=CD，
∴∠CAD=60°，
∴∠BAD=120°，
∵E为BC的中点，
∴AE⊥BC，∠EAC=30°，
∴AE=，
同理：AF=，
∵AE=AF，∠CAF=30°
∴∠EAF=60°，
∴△AEF是等边三角形，
∴EF=，
∴△AEF的周长为3．
故答案为：3．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
