题目内容
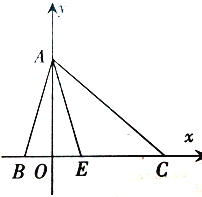
【题目】如图,点B,E关于y轴对称,且E在AC的垂直平分线上,已知点C(5,0).
(1)如果∠BAE=40°,那么∠C= °;
(2)如果△ABC的周长为13cm,AC=6cm,那么△ABE的周长= cm;
(3)AB+BO= .
【答案】(1)35;(2)7;(3)5.
【解析】试题分析:
(1) 根据轴对称的性质可知,△ABE是等腰三角形. 根据三角形的内角和,容易得到∠AEB的度数. 根据线段垂直平分线的相关结论,可以得到∠C=∠CAE. 通过三角形外角的相关结论,不难求得∠C的度数.
(2) 根据线段垂直平分线的相关结论可知AE=EC. 因此,△ABE的周长为AB+BC. 由△ABC的周长和边AC的长,不难求得AB+BC的长,进而得到△ABE的周长.
(3) 根据前两个小题的解题过程可知,AB=AE,AE=EC. 由轴对称的性质可得BO=EO. 结合上述两个条件可知,AB+BO=EC+EO=OC. 由于线段OC的长代表了点C的横坐标值,所以利用点C的坐标即可得到AB+BO的值.
试题解析:
(1) ∵点B与点E关于y轴对称,
∴BO=EO,AO⊥BE,
∴AB=AE.
∵∠BAE=40°,AB=AE,
∴在△ABE中,![]() .
.
∵点E在AC的垂直平分线上,
∴AE=EC,
∴∠C=∠CAE.
∵∠AEB是△AEC的一个外角,
∴∠AEB=∠C+∠CAE=2∠C=70°,
∴∠C=35°.
故本小题应填写:35.
(2) ∵△ABC的周长为13cm,
∴AB+BC+AC=13cm,
∵AC=6cm,
∴AB+BC=13-6=7(cm).
∵△ABE的周长为AB+BE+AE,
又∵AE=EC,
∴AB+BE+AE=AB+BE+EC=AB+BC.
∴△ABE的周长为7cm.
故本小题应填写:7.
(3) ∵AB=AE,AE=EC,
∴AB=EC.
∵BO=EO,
∴AB+BO=EC+EO=OC.
∵点C的坐标为(5, 0),
∴OC=5.
故本小题应填写:5.

 阅读快车系列答案
阅读快车系列答案