��Ŀ����
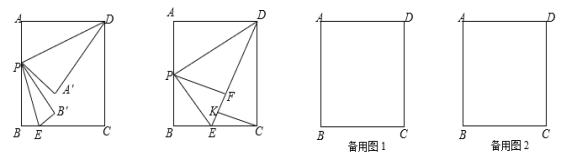
����Ŀ����ͼ���ھ���ABCD�У�AB��8��BC��6����P����E�ֱ��DZ�AB��BC�ϵĶ��㣬����DP��PE������ADP����BPE�ֱ���DP��PE�۵�����A���B�ֱ����ڵ�A����B������
(1) ����P�˶�����AB���е㴦ʱ����A�����B���غ��ڵ�F��������C��CK��EF��K����CK�ij���
(2) ����P�˶���ijһʱ�̣���P��A'��B'����ǡ����ͬһֱ���ϣ���A'B'��4 �������ʱAP�ij���
���𰸡���1��![]() ����2��,PA�ij�Ϊ2��6��
����2��,PA�ij�Ϊ2��6��
��������
��1�����۵������ʿɵ�E ,F,D������ͬһֱ���ϣ���Rt��DEC��,���ݹ��ɶ��������BE��CE��DE�ij����ٸ���������������CK��ֵ��
��2������������������ۣ�����A��B����4�г�������⼴��.
����ͼ��
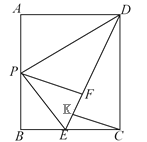
���ı���ABCDΪ���Σ�����ADP����BPE�ֱ���DP��PE�۵���
���PFD����PFE��90��,
���PFD����PFE��180��,����E ,F,D������ͬһֱ���ϣ�
��BE��EF��x,��EC��6��x,
��DC��AB��8, DF��AD��6,
��Rt��DEC��,��DE��DF��FE��6��x, EC��6��x, DC��8,
��(6��x)2��(6��x)2��82,
����ó�x=![]() ,��BE��EF��
,��BE��EF��![]() ,
,
��DE��![]() , EC��
, EC��![]() ,
,
��S��DCE��![]() DCCE��
DCCE��![]() DECK,
DECK,
��CK��![]() ��
��
�Ƣ���ͼ2��,��AP��x,��PB��8��x,
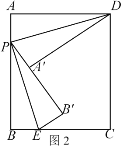
���۵���֪��PA����PA��x , PB����PB��8��x,
��A��B����4,
��8��x��x��4,
��x��2, ��AP��2��
����ͼ3��,
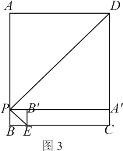
��A��B����4,
��x��(8��x)��4, ��x��6, ��AP��6��
��������,PA�ij�Ϊ2��6��

 ��������������������ϵ�д�
��������������������ϵ�д�