题目内容
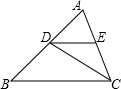如图，已知△ABC的角平分线CD交AB于D，DE∥BC交AC于E，若DE=3，AE=4，则AC=7
7
．分析：根据角平分线的定义可得∠BCD=∠DCE，再根据两直线平行，内错角相等可得∠BCD=∠CDE，然后求出∠DCE=∠CDE，再根据等角对等边可得CE=DE，然后根据AC=AE+CE代入数据计算即可得解．
解答：解：∵CD是∠ACB的平分线，
∴∠BCD=∠DCE，
∵DE∥BC，
∴∠BCD=∠CDE，
∴∠DCE=∠CDE，
∴CE=DE，
∵DE=3，AE=4，
∴AC=AE+CE=4+3=7．
故答案为：7．
∴∠BCD=∠DCE，
∵DE∥BC，
∴∠BCD=∠CDE，
∴∠DCE=∠CDE，
∴CE=DE，
∵DE=3，AE=4，
∴AC=AE+CE=4+3=7．
故答案为：7．
点评：本题考查了等腰三角形的判定与性质，角平分线的定义，平行线的性质，熟记性质并求出CE=DE是解题的关键．
练习册系列答案
相关题目
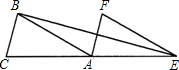如图，已知△ABC的面积为4，且AB=AC，现将△ABC沿CA方向平移CA的长度，得到△EFA．
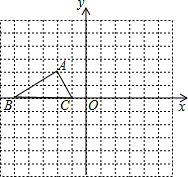（2010•孝感模拟）如图，已知△ABC的三个顶点的坐标分别为A（-2，2）、B（-5，0）、C（-1，0）．
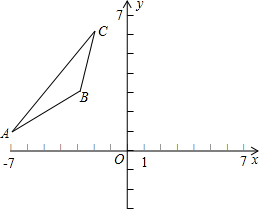如图，已知△ABC的三个顶点的坐标分别是A（-7，1），B（-3，3），C（-2，6）．