Question

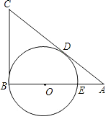
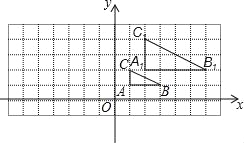
【题目】如图，在第一象限内作射线，与轴的夹角为，在射线上取点，过点作轴于点．在抛物线上取点，在轴上取点，使得以，，为顶点，且以点为直角顶点的三角形与全等，则符合条件的点的坐标是________．

Answer 1

【答案】，

【解析】

由于AH的长度没有确定，所以只要以点Q为直角顶点的三角形与△AOH相似，那么两者就有可能全等；当点Q为直角顶点时，若∠POQ=30°或∠POQ=60°时，都符合解题要求，那么可根据∠POx的度数求出直线OP的解析式，然后联立抛物线的解析式即可得点P的坐标．

解：在Rt△AOH中，∠AOH=30°；
由题意，可知：当∠POQ=30°或∠POQ=60°时，以点Q为直角顶点的△POQ与△AOH全等，故∠POx=60°或∠POx=30°；
①当∠POx=60°时，kOP=tan60°=，所以，直线OP：y=x，联立抛物线的解析式， ,解得： 或

即P，

②当∠POx=30°时，kOP=tan30°=，所以，直线OP：y=x，联立抛物线的解析式，,解得： 或

即P.