Question

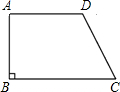
如图，在梯形ABCD中，AB∥DC，∠D=90°，AD=DC=4，AB=1，F为AD的中点，则点F到BC的距离是（　　）

A．2

B．4

C．8

D．1

Answer 1

连接BF，CF，过A作AE∥BC，过F作FG⊥BC于G，
则四边形ABCE是平行四边形，AE=BC，AB=CE=1，DE=DC-CE=4-1=3，
∵∠D=90°，
∴△ADE是直角三角形，
由勾股定理得AE=

AD2+DE2

=

42+32

=5，
∵AE=BC，
∴BC=5，
∵AB∥DC，∠D=90°，F为AD的中点，AD=DC=4，AB=1，
∴AF=FD=

1

2

AD=

1

2

×4=2，△DCF与△ABF是直角三角形，CF=

CD2+DF2

=

42+22

=2

5

；
BF=

AB2+AF2

=

12+22

=

5

；
在△BFC中，
∵BF²+CF²=（

5

）²+（2

5

）²=25=BC²=5²=25，
∴△BFC是直角三角形；
∴S_△BFC=

1

2

BF•CF=

1

2

BC•FG，即

5

•2

5

=5FG，FG=2．
故选A．