��Ŀ����
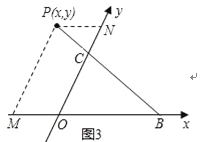
����Ŀ��������ƽ��ֱ������ϵ����ͼ1����ƽ���ڣ����ԭ���غϵ����������ֱ����ô���dz�����������ϵΪб����ϵ����P��б����ϵxOy�е�����һ�㣬����P�ֱ������������ƽ���ߣ���x�ᡢy�ύ�ڵ�M��N�����M��N��x�ᡢy���Ϸֱ��Ӧ��ʵ����a��b����ʱ��P������Ϊ��a��b����
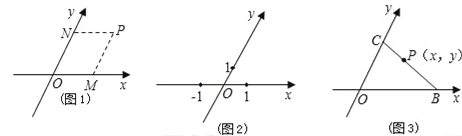
��1����ͼ2����б����ϵxOy�У�������A����2��3����
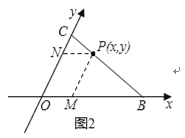
��2����ͼ3����б����ϵxOy�У���֪��B��5��0����C��0��4������P��x��y�����߶�CB�ϵ�����һ�㣬��y��x֮��ĵ�����ϵʽΪ ��
��3������2���еĵ�P���߶�CB���ӳ����ϣ��������������䣬���жϣ�2���еĽ����Ƿ���Ȼ��������˵�����ɣ�
���𰸡���1������������2��3x+4y=12����3����Ȼ����
��������
�����������1����AM��y�ᣬAM��x�ύ�ڵ�M��AN��x�ᣬAN��y�ύ�ڵ�N����������AMON��Ȼ��������ε������Լ��ȱ������ε��ж�����������OA�ij��ȣ�
��2������P�ֱ������������ƽ���ߣ���x�ᡢy�ύ�ڵ�M��N���� PN=x��PM=y������ƽ���߽��߶γɱ����ֱ��г�����x��y�ı���ʽ![]() ��
��![]() �������߶μ�ĺͲ��ϵ���PC+BP=BC֪
�������߶μ�ĺͲ��ϵ���PC+BP=BC֪![]() ��
��
��3������P���߶�BC���ӳ�����ʱ������������Ȼ�������������£���ʱ PN=��x��PM=y��֤������ͬ��2����
��1����AM��y�ᣬAM��x�ύ�ڵ�M��AN��x�ᣬAN��y�ύ�ڵ�N����������AMON��Ȼ��������ε������Լ��ȱ������ε��ж�����������OA�ij��ȣ�
��2������P�ֱ������������ƽ���ߣ���x�ᡢy�ύ�ڵ�M��N���� PN=x��PM=y������ƽ���߽��߶γɱ����ֱ��г�����x��y�ı���ʽ![]() ��
��![]() �������߶μ�ĺͲ��ϵ���PC+BP=BC֪
�������߶μ�ĺͲ��ϵ���PC+BP=BC֪![]() ��
��
��3������P���߶�BC���ӳ�����ʱ������������Ȼ�������������£���ʱ PN=��x��PM=y��֤������ͬ��2����
�����������1����ͼ1��AM��y�ᣬAM��x�ύ�ڵ�M��AN��x�ᣬAN��y�ύ�ڵ�N��
���ı���AMONΪƽ���ı��Σ���OM=ON��
��AMON������OM=AM
��OAƽ�֡�MON��
�֡ߡ�xOy=60�㣬
���MOA=60�㣬
���MOA�ǵȱ������Σ�
��OA=OM=2��
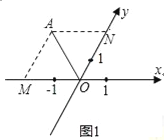
��2������P�ֱ������������ƽ���ߣ���x�ᡢy�ύ�ڵ�M��N��
�� PN=x��PM=y��
��PN��OB����![]() ��
��![]() ��
��
��PM��OC����![]() ����
����![]() ��
��
��![]() ��
��
�� 3x+4y=12��
�ʴ�Ϊ��3x+4y=12��
��3����2���еĽ�����Ȼ��������ͼ3������P���߶�BC���ӳ�����ʱ������������Ȼ�������������£���ʱ PN=��x��PM=y��
�루2�����ƣ�![]() ��
��![]() ��
��
�֡�![]() ��
��
��![]() ��
��![]() ��
��