题目内容
【题目】已知:AB是⊙O的直径,点P在线段AB的延长线上,BP=OB=2,点Q在⊙O上,连接PQ.
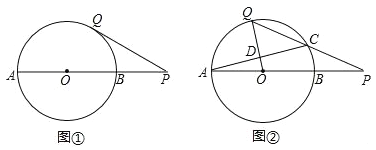
(1)如图①,线段PQ所在的直线与⊙O相切,求线段PQ的长;
(2)如图②,线段PQ与⊙O还有一个公共点C,且PC=CQ,连接OQ,AC交于点D.
①判断OQ与AC的位置关系,并说明理由;
②求线段PQ的长.
【答案】(1)![]() ;(2)①OQ⊥AC,理由见试题解析;②
;(2)①OQ⊥AC,理由见试题解析;②![]() .
.
【解析】试题分析:(1)如图①,连接OQ.利用切线的性质和勾股定理来求PQ的长度;
(2)如图②,连接BC.由三角形中位线得到BC∥OQ.利用圆周角定理得到BC⊥AC,故OQ⊥AC;
(3)利用割线定理来求PQ的长度.
试题解析:(1)如图①,连接OQ.∵线段PQ所在的直线与⊙O相切,点Q在⊙O上,∴OQ⊥OP.又∵BP=OB=OQ=2,∴PQ=![]() =
=![]() =
=![]() ,即PQ=
,即PQ=![]() ;
;
(2)OQ⊥AC.理由如下:如图②,连接BC.∵BP=OB,∴点B是OP的中点,又∵PC=CQ,∴点C是PQ的中点,∴BC是△PQO的中位线,∴BC∥OQ.又∵AB是直径,∴∠ACB=90°,即BC⊥AC,∴OQ⊥AC;
(3)如图②,PCPQ=PBPA,即![]() =2×6,解得PQ=
=2×6,解得PQ=![]() .
.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目