题目内容
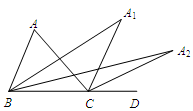
(1)如图,ΔABC中,∠ABC=50°,∠ACB=70°,D为边BC上一点(D与B、C不重合),连接AD,∠ADB的平分线所在直线分别交直线AB、AC于点E、F. 求证:2∠AED-∠CAD=170°;
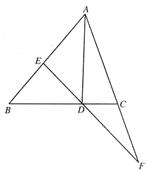
(2)若∠ABC=∠ACB=n°,且D为射线CB上一点,(1)中其他条件不变,请直接写出∠AED与∠CAD的数量关系.(用含n的代数式表示)

(2)若∠ABC=∠ACB=n°,且D为射线CB上一点,(1)中其他条件不变,请直接写出∠AED与∠CAD的数量关系.(用含n的代数式表示)
(1)根据角平分线的性质可设∠ADE=∠BDE=x°,由∠AED=∠ABC+∠BDE,∠ABC=50°可得∠AED= x°+50°①,根据三角形的外角的性质可得∠ADB=∠ACB+∠CAD,即可得到∠CAD=∠ADB-∠ACB,由∠ACB=70°,∠ADB=(2x)°可得∠CAD=(2x)°-70°②,由①×2-②即可证得结论;
(2)2∠AED-∠CAD=(3n)°或2∠AED+∠CAD=540°-(3n)°.
(2)2∠AED-∠CAD=(3n)°或2∠AED+∠CAD=540°-(3n)°.
试题分析:(1)根据角平分线的性质可设∠ADE=∠BDE=x°,由∠AED=∠ABC+∠BDE,∠ABC=50°可得∠AED= x°+50°①,根据三角形的外角的性质可得∠ADB=∠ACB+∠CAD,即可得到∠CAD=∠ADB-∠ACB,由∠ACB=70°,∠ADB=(2x)°可得∠CAD=(2x)°-70°②,由①×2-②即可证得结论;
(2)解法同(1).
解:(1)DE平分∠ADB
∴设∠ADE=∠BDE=x°
∵∠AED=∠ABC+∠BDE,∠ABC=50°
∴∠AED= x°+50° ①
∵∠ADB=∠ACB+∠CAD
∴∠CAD=∠ADB-∠ACB
∵∠ACB=70°,∠ADB=(2x)°
∴∠CAD=(2x)°-70° ②
∴由①×2-②,得:2∠AED-∠CAD=170°;
(2)2∠AED-∠CAD=(3n)°或2∠AED+∠CAD=540°-(3n)°.
点评:此类问题难度较大,在中考中比较常见,一般在压轴题中出现,需特别注意.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
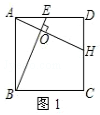
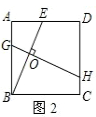
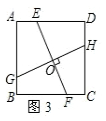
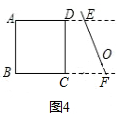
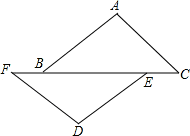
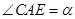
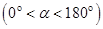
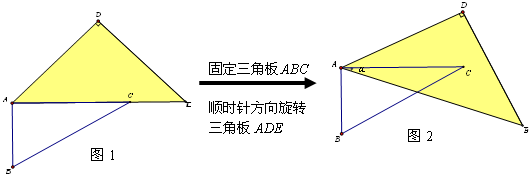
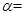 _____时,AD∥BC,在图3中画出相应图形;
_____时,AD∥BC,在图3中画出相应图形;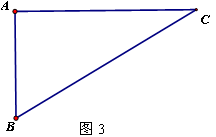
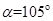 ,此时DE∥BC,请你写出除(1)和
,此时DE∥BC,请你写出除(1)和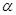 的所有可能的度数________________.
的所有可能的度数________________.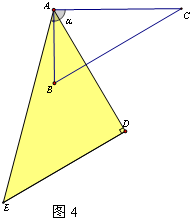
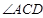 是
是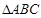 的外角,
的外角,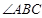 的平分线与
的平分线与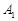 ,
,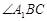 的平分线与
的平分线与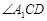 的平分线交于点
的平分线交于点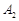 ,……,
,……,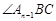 的平分线与
的平分线与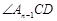 的平分线交于点
的平分线交于点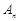 ,设
,设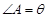 ,则
,则 ;
; .
.