题目内容
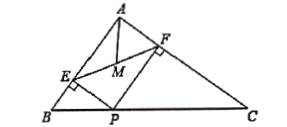
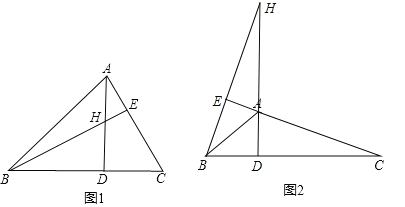
【题目】如图(1)△ABC中,H是高AD和BE的交点,且AD=BD.
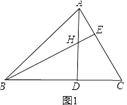
(1)请你猜想BH和AC的关系,并说明理由;
(2)若将图(1)中的∠A改成钝角,请你在图(2)中画出该题的图形,此时(1)中的结论还成立吗?(不必证明).

【答案】(1)证明见解析;(2)成立,理由见解析.
【解析】(1)BH=AC;证明△BDH≌△ADC即可;
(2)成立.证明思路同(1).
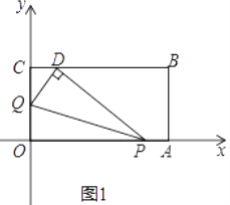
(1)BH=AC;如图1.
∵AD和BE是△ABC的高,∴∠BDH=∠ADC=90°,∠DBH+∠C=∠CAD+∠C=90°,∴∠DBH=∠DAC.在△BDH和△ADC中,∵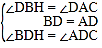 ,∴△BDH≌△ADC(ASA),∴BH=AC;
,∴△BDH≌△ADC(ASA),∴BH=AC;
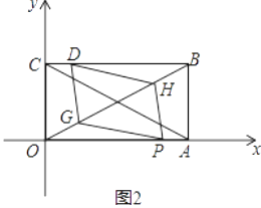
(2)成立,如图2.
∵AD和BE是△ABC的高,∴∠BDH=∠ADC=90°,∠DBH+∠H=∠DBH+∠C=90°,∴∠H=∠C.在△BDH和△ADC中,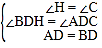 ,∴△BDH≌△ADC(AAS),∴BH=AC.
,∴△BDH≌△ADC(AAS),∴BH=AC.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
【题目】正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):
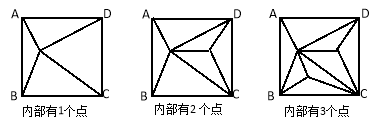
(1)填写下表:
正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | … | n |
分割成的三角形的个数 | 4 | 6 | … |
(2)原正方形能否被分割成2016个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.