题目内容
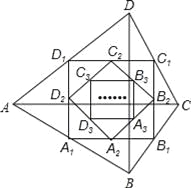
【题目】八个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这八个正方形分成面积相等的两部分,则该直线l的解析式为( )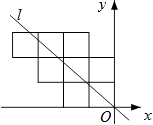
A.y=﹣x
B.y=﹣ ![]() x
x
C.y=﹣ ![]() x
x
D.y=﹣ ![]() x
x
【答案】D
【解析】解:设直线l和八个正方形的最上面交点为A,过A作AB⊥OB于B,B过A作AC⊥OC于C,
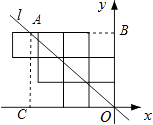
∵正方形的边长为1,
∴OB=3,
∵经过原点的一条直线l将这八个正方形分成面积相等的两部分,
∴S△AOB=4+1=5,
∴ ![]() OBAB=5,
OBAB=5,
∴AB= ![]() ,
,
∴OC= ![]() ,
,
由此可知直线l经过(﹣ ![]() ,3),
,3),
设直线方程为y=kx,
则3=﹣ ![]() k,
k,
k=﹣ ![]() ,
,
∴直线l解析式为y=﹣ ![]() x,
x,
故答案为:D.
观察图像可知该直线是正比例函数,根据题意求出图像上一点坐标,即可求出此函数解析式。

练习册系列答案
相关题目