题目内容
【题目】如图在四边形ABCD中，∠A=90°，AD=6，AB=8,BC=26,CD=24
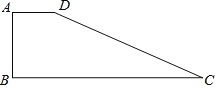
（1）求四边形ABCD的面积．
（2）求D到BC的距离．
【答案】（1）336；（2）
【解析】
可以作 出辅助线，从而得出两个直角三角形，运用已知条件的出答案，D到BC的距离可以做D到BC的高线，运用面积的表示方法可以求得高.
(1)连接线段BD，
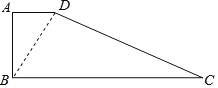
在Rt△ABD中，AD=6，AB=8，
∴BD=10，
在△BCD中，BD=10，CD=24，BC=26，
∴BD2+CD2=BC2，
∴△BCD为直角三角形，
∴S四边形ABCD=S△ABD+S△BCD=
ADAD+BDCD=24+312=336；
(2)设D到BC的距离为x，
∴24×10×=×26x
∴x=，
∴D到BC的距离为.
练习册系列答案
相关题目
