题目内容
【题目】如图,△ABC是边长为4cm的等边三角形,动点P从点A出发,以2cm/s的速度沿A→C→B运动,到达B点即停止运动,过点P作PD⊥AB于点D,设运动时间为x(s),△ADP的面积为y(cm2),则能够反映y与x之间函数关系的图象大致是( )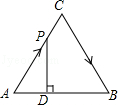
A.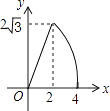
B.
C.
D.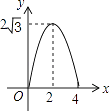
【答案】B
【解析】解:过点P作PD⊥AB于点D,△ABC是边长为4cm的等边三角形,
则AP=2x,
当点P从A→C的过程中,AD=x,PD= ![]() x,如右图1所示,
x,如右图1所示,
则y= ![]() ADPD=
ADPD= ![]() =
= ![]() ,(0≤x≤2),
,(0≤x≤2),
当点P从C→B的过程中,BD=(8﹣2x)× ![]() =4﹣x,PD=
=4﹣x,PD= ![]() (4﹣x),PC=2x﹣4,如右图2所示,
(4﹣x),PC=2x﹣4,如右图2所示,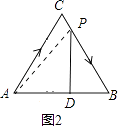
则△ABC边上的高是:ACsin60°=4× ![]() =2
=2 ![]() ,
,
∴y=S△ABC﹣S△ACP﹣S△BDP
= ![]() ﹣
﹣ ![]() =
= ![]() (2<x≤4),
(2<x≤4),
故选B.
过点P作PD⊥AB于点D,分类求出点P从A→C和从C→B函数解析式,即可得到相应的函数图象.

练习册系列答案
相关题目