题目内容
【题目】如图, ![]() 是
是![]() 的直径,
的直径, ![]() 的平分线交
的平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的切线
的切线![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .
.
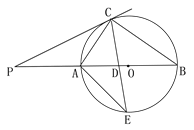
(1)求证: ![]() ;
;
(2)若![]() ,
, ![]() ,求线段
,求线段![]() 、
、![]() 的长.
的长.
【答案】(1)见解析;(2)![]() ,
, ![]()
【解析】试题分析:(1)连接OC、OE.由PC为⊙O的切线,得到∠PCO=90°.再由CE平分∠ACB,得到E为弧AB的中点,进一步得到∠AOE=90°. 由OC=OE,得到∠OEC=∠OCE, 可以得到∠PCD=∠PDC,即可得到结论;
(2)过点A作AQ⊥CE,垂足为Q.在Rt△ABC中,由勾股定理得到AB的长,进而得到半径OA和OE的长.在Rt△AOE中,由AO=OE,可以得到AE的长,由Rt△AQC是等腰直角三角形,可以求得AQ、CQ的长,由勾股定理得到QE的长,进而得到CE的长.
试题解析:(1)证明:连接![]() 、
、![]() .
.
∵![]() 为
为![]() 的切线,∴
的切线,∴![]() .
.
又∵![]() 平分
平分![]() ,∴
,∴![]() 为弧
为弧![]() 的中点,∴
的中点,∴![]()
∵![]() ,
, ![]() ,
,
又∵![]() ,∴
,∴![]() ,
,
∴![]() ,即
,即![]() ;
;

(2)过点![]() 作
作![]() ,垂足为
,垂足为![]() .
.
∵![]() 为
为![]() 的直径,∴
的直径,∴![]() ,
,
∴![]() ,
,
∴![]()
在![]() 中,
中, ![]()
在![]() 中,
中, ![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]()
在![]() 中,
中, ![]() ,
,
故![]()

练习册系列答案
相关题目



