Question

【题目】已知关于x的一元二次方程x2﹣（m+1）x+（m2+1）＝0有两个相等的实数根．

（1）求m的值；

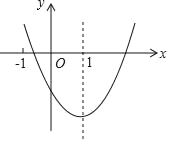
（2）将y＝﹣x2+（m+1）x﹣（m2+1）的图象向左平移3个单位长度，再向上平移2个单位长度，写出变化后函数的表达式；

（3）在（2）的条件下，当直线y＝2x+n与变化后的图象有公共点时，求n2﹣4n的最小值

Answer 1

【答案】（1）m的值为1；（2）y＝﹣x2﹣4x﹣2；（3）﹣4．

【解析】

（1）根据判别式的意义得到△＝（m+1）2﹣4（m2+1）＝0，然后解方程即可；

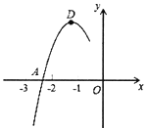
（2）把原抛物线解析式配成顶点式得到y＝﹣（x﹣1）2，则它的顶点坐标为（1，0），利用点平移的规律得到平移后抛物线的顶点坐标为（﹣2，2），然后利用顶点式写出变化后函数的表达式；

（3）根据题意方程﹣x2﹣4x﹣2＝2x+n有实数解，则利用判别式的意义得到n≤7，再配方得到n2﹣4n＝（n﹣2）2﹣4，然后根据二次函数的性质进行问题．

（1）△＝（m+1）2﹣4（m2+1）＝0，解得：m1＝m2＝1，即m的值为1；

（2）原抛物线解析式为y＝﹣x2+2x﹣1，即y＝﹣（x﹣1）2，它的顶点坐标为（1，0），把点（1，0）向左平移3个单位长度，再向上平移2个单位长度后的对应点的坐标为（﹣2，2），所以变化后函数的表达式为y＝﹣（x+2）2+2，即y＝﹣x2﹣4x﹣2；

（3）﹣x2﹣4x﹣2＝2x+n，整理得：x2+6x+n+2＝0，△＝62﹣4（n+2）≥0，解得：n≤7，n2﹣4n＝（n﹣2）2﹣4，所以当n＝2时，n2﹣4n的值最小，n2﹣4n最小值为﹣4．