题目内容
【题目】已知,如图所示的正方形网格中,每个网格的单位长度为1,△ABC的顶点均在格点上,根据所给的平面直角坐标系解答下列问题:
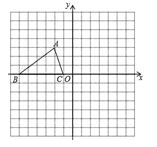
(1)A点的坐标为________;B点的坐标为________;C点的坐标为________.
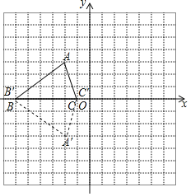
(2)将点A、B、C的横坐标保持不变,纵坐标分别乘以-1,分别得点A'、B'、C',并连接A'、B'、C'得△A' B' C',请画出△A' B' C'.
(3)△A' B' C'与△ABC的位置关系是________.
【答案】(1)(-2,3),(-6,0),(-1,0);(2)答案见解析;(3)关于x轴对称
【解析】
(1)根据各点在坐标系中的位置即可得出结论,注意坐标规律(横坐标、纵坐标);
(2)把点A,B,C的横坐标保持不变,纵坐标分别乘以-1,分别得点A′,B′,C′坐标,并在图上找到各点连接A′,B′,C′得△A′B′C′即可;
(3)根据△A′B′C′与△ABC在坐标系中的位置即可得出结论,也可根据坐标关系判断,关于x轴对称横坐标不变,纵坐标互为相反数.
解:(1)A点的坐标为(-2,3);B点的坐标为(-6,0);C点的坐标为(-1,0);
(2)A′点的坐标为(-2, -3);B′点的坐标为(-6,0);C′点的坐标为(-1,0),如图△A′B′C′即为所求;
(3)由图可知,△A′B′C′与△ABC的位置关于x轴对称.
故答案为:关于x轴对称.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目