题目内容
如图,在等腰梯形ABCD中,AB∥CD,AD=BC=2,∠A=60°,BD平分∠ABC,则这个梯形的周长是____.
10
分析:根据平行线的性质推出∠CDB=∠DBA,得出∠CDB=∠CBD,推出DC=BC,过D作DE∥BC交AB于E,推出四边形DEBC是平行四边形,得出DC=BE,DE=BC,∠DEA=∠CBA,证△ADE是等边三角形,求出AE即可.

解:∵DC∥AB,
∴∠CDB=∠DBA,
∵BD平分∠ABC,
∴∠CBD=∠DBA,
∴∠CDB=∠CBD,
∴DC=BC=2cm,
过D作DE∥BC交AB于E,
∵DC∥AB,DE∥BC,
∴四边形DEBC是平行四边形,
∴DC=BE,DE=BC,∠DEA=∠CBA,
∵DC∥AB,AD=BC,
∴∠A=∠CBA=∠DEA=60°,
∴AD=DE,
∴△ADE是等边三角形,
∴AE="AD=2" ,
∴这个梯形的周长是AB+BC+CD+AD="2" +2 + 2 + 2 +2 =10,
故答案为:10.

练习册系列答案
相关题目
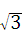 ,点O是AB的中点,点P在AB的延长线上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点发发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0).
,点O是AB的中点,点P在AB的延长线上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P点发发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动,在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧.设运动的时间为t秒(t≥0).
 ,则它的边数是
,则它的边数是 中,
中, ,
, 平分
平分 ,
, 交
交 于
于 .
.
 是菱形;
是菱形; 的形状,并说明理由.
的形状,并说明理由. 中,
中, 为
为 的中点,
的中点, 于
于 ,交
,交 于点
于点 ,交
,交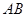 于点
于点 ,连接
,连接 、
、 。有如下结论:①
。有如下结论:①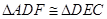 ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤ 。其中正确的结论的个数为( )
。其中正确的结论的个数为( )
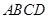 的对角线相交于点
的对角线相交于点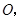 请你添加一个条件: ,使其为正方形
请你添加一个条件: ,使其为正方形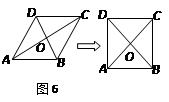
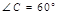 ,BD平分
,BD平分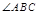 ,如果这个梯形的周长为30,则AB的长为( )
,如果这个梯形的周长为30,则AB的长为( )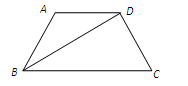
 中,
中, 为
为 的中点,连接
的中点,连接 并延长交
并延长交 的延长线于点
的延长线于点 ,则图中全等的直角三角形共有 ( )
,则图中全等的直角三角形共有 ( )